随着深度学习在各项研究中展现出的突出优势,深度学习模型的云服务也在飞速发展。在云模型的应用中,始终存在着客户端个人隐私数据和服务端云模型之间的隐私保护问题。一方面,客户端需要防备服务端对个人数据的收集;另一方面,服务端也需要防备客户端发起的模型窃取等问题。
模型的推理需要输入数据和模型参数共同参与一系列复杂运算,而如何解决高效推理和隐私保护这一对矛盾也就成了问题研究的关键。在对两方数据进行安全保护的基础上,相关研究人员对深度学习的安全推理进行了深入研究,提出了一系列基于以同态加密为主的隐私保护方法,并在保证安全性和正确性的前提下对模型推理进行了算法改良,使加密过程带来的时间开销得以大幅减少,从而使安全推理具备实际应用的可能。
本文针对深度学习安全推理这一问题,对相关的文献进行综述,整理了以同态加密为主的多种隐私计算方法在安全推理中的应用,并重点阐述了有关研究人员在加密基础上对优化时间开销做出的贡献。
引言
近年来,随着学术研究的推进和各项高效模型的提出,深度学习方法飞速发展,并在一系列任务上展现了远超传统方法的能力。深度学习的实际应用也成为了目前业界十分关心的话题。由于深度学习模型的复杂性,常常需要在高性能配置的环境下进行推理,因此在众多深度学习应用中,深度学习云服务的模式备受各方青睐。
但是随之产生了一个重要的问题,即如何在客户端——服务端两方之间进行隐私保护的问题。一方面,客户端需要将个人数据上传到服务端,在数据传输和到达云端的过程中存在泄漏的风险,即使在服务端也有可能遭到服务端对数据的非法采集和利用;另一方面,服务端所部署的深度学习模型往往基于服务方所收集的数据集进行训练,因此服务端也需要防备对客户端对模型的窃取和攻击,特别是防止客户端通过中间推理结果反向推断模型的参数,导致服务端模型泄漏。
在此基础上,系列研究人员提出了基于加密方法的深度学习推理过程,应用同态加密和安全两方计算等隐私计算方法,使得两方的数据在安全加密的情况下进行推理,从而提出了对于此问题的初步解决方案。但是进行加密推理后的代价是模型的推理速度下降了几个数量级,这意味着完全无法在实际部署的云模型中提供有效的服务能力。因此安全推理和高效计算的矛盾成为了该领域的研究核心。
对于这一矛盾,有关学者给出了一系列的优化方法,以尽可能地降低加密过程所带来的额外时间开销。在对该问题进行优化的过程中,研究人员注意到了深度学习模型的结构特性,并针对模型中重点出现的矩阵运算、卷积、池化、激活函数等结构选择了合适的加密算法。在后续的研究中,有关学者发现了单指令多数据方法在批量运算中所带来的收益,并在保证正确性的前提下,通过调整相关的运算顺序,提高模型推理的速度。后续的研究中,有学者通过引入加密方法下的多项式运算代替原有的矩阵运算,从而进一步地降低了时间开销。
在上面的方法中,推理过程需要客户端和服务端两方共同参与,因此对模型的实际应用仍然带来了不小的挑战。近期有学者开始关注全同态加密方法在深度学习模型推理中的应用,并通过对深度神经网络结构的调整,使得客户端无需参与中间推理过程,而只需要上传加密后的数据即可获知模型的最终推理结果,这也为安全推理提供了新的研究路径。
本文从深度学习安全推理的主题出发,首先介绍在信息安全领域中常见的隐私计算方法和概念,之后介绍加密方法在深度学习推理中的应用,以及各项研究工作在优化安全推理的时间开销方面做出的努力。
隐私计算方法
随着计算机的广泛应用,在数据处理的问题上,隐私保护已经成为一个至关重要的话题。近年来,随着相关研究人员对这一问题的不断深入研究,逐渐总结为一个较为完善的计算方法体系,即隐私计算。隐私计算结合了密码学、统计学等多门学科,其发展关系到信息安全领域的一系列重要话题。在深度学习安全推理的实现中,绝大多数方法基于目前对隐私计算的相关研究,因此本文首先需要介绍隐私计算的相关方法,具有代表性的方法为同态加密、秘密共享和混淆电路。
同态加密
同态加密指的是这样一类加密方法:我们支持在加密的基础上进行系列运算,这些运算在密文域进行,但是可以对应到明文域上的相应运算,故而当解密后可以得到正确的运算的结果。这个过程可以用经典的“珠宝店”问题来比喻,珠宝店主希望工人能把店里的金子加工成漂亮的首饰,又不希望金子在这个过程中被盗走,因此把金子放在密闭的盒子里,工人只能通过两端的窗口伸入手套来完成加工,而无法将盒子中的金子带走。
同态加密的方案常常是非对称的,即加密操作使用公钥,解密操作使用私钥。公钥可以分发给其他人参与到加密过程中,而只有自己可以进行解密。同态加密并不是一个容易构造的加密方式,其研究的历史是从部分同态加密开始的。我们可以看到在一些加密方案中对某些运算存在着同态性质。如El-Gamal方案基于离散对数算法的难题,它支持乘法同态,即 $Enc(pt_1) \cdot Enc(pt_2) = Enc(pt_1 \cdot pt_2)$ 。后面Paillier提出了经典的概率同态加密方案,但该方案也是部分同态的。在同态加密研究数十年后,终于有学者提出了全同态加密的方案,即可以支持无限制的各类同态操作,这也极大促进了同态加密的相关应用。
深度学习安全推理地过程中极大地依赖同态加密方案,因为深度学习模型涉及到非常多的矩阵运算,这些运算又是基于加法和乘法的,因此引入一个支持同态加法和同态乘法的加密方案可以较好地实现这些操作。
秘密共享
秘密共享是共享密码相关的一种技术,我们同样可以用一个经典的“遗产继承”寓言来解释秘密共享的含义。一个富翁希望让自己的遗产交给三个儿子来共同打理:如果只把钥匙交给其中一个儿子,那么其他的两个儿子就要吃亏;因此可以把钥匙分成三份,只有当三个人同时到场才能生效,这样可以避免一人独占的问题;而为了防备紧急情况下其中一人正好不在,进一步地可以将生效机制设置为只要有任意两把钥匙即可,但单独一人的钥匙无法起作用。秘密共享也是这样的原理,我们将一份秘密分开给不同的参与方分别保存,而只有一定集合内的参与方共同授权时,共享的秘密才能被恢复。
这一方式在深度学习安全推理中是非常常用的,因为在加密基础上进行深度学习的过程中常常需要保存中间的计算结果,如果单纯地把中间结果交给服务端,那么服务端就可以通过自己的模型参数反向的推理出客户端的数据输入,造成客户隐私泄漏的问题;而如果单纯的把中间结果交给客户端,那么客户端就可以利用中间结果对服务端的模型参数进行推断,甚至通过这样的攻击方式实现模型窃取。客户端和服务端之间的这一对矛盾使得常常需要将中间结果共享地交给两方来保存,而不是单纯地保留给其中的一方。
混淆电路
混淆电路最早要追溯到上世纪八十年代姚期智先生提出的“百万富翁”问题,即两个百万富翁在互相不知道对方财富的情况下,如何通过两方计算比较出二者谁的的财富更多。姚期智先生对这一问题给出了创造性的解决方案,即混淆电路方案。混淆电路是一种在电路层面进行安全两方计算的协议,由混淆电路生成方和运算方组成,首先生成方将运算任务通过电路表示,并进行混淆操作,电路的输入输出和中间结果都是密文,然后生成方将混淆电路发送给运算方,后者使用密文进行运算并将密文结果返回给生成方。生成方通过解密得到运算结果,并将结果告知其他参与方。
混淆电路的一大优势是其计算代价较小,且可以支持较为复杂的运算,包括一些复杂的逻辑门运算等。但是缺点是混淆电路无法复用。但由于混淆电路能够支持一些复杂的非线性操作,在深度学习安全推理问题中,混淆电路也常常是完成安全推理的重要一环,并且常常用在完成某些复杂的运算上。
深度学习模型结构和安全推理
深度神经网络由不同的层组成,每一层获得来自上游的输出,并将运算结果传递给下游。神经网络的不同层的不同结构决定了在安全推理中的方法的差异,因此在介绍安全推理方法之前,我们需要首先梳理深度学习模型的结构,并初步分析其与安全推理之间的关系。
线性部分
神经网络中有大量线性变换,最常见的是矩阵向量乘法和加法:$\textbf{y=Wx+b}$ 。其中 $\mathbf{x} \in \mathbb{R}^{l\times 1} $ 是输入,$\mathbf{W} \in \mathbb{R}^{n\times l} $ 是权重矩阵, $\mathbf{y} \in \mathbb{R} ^{n \times 1}$ 是输出,这常见于全连接层中,是最初等的神经网络操作,其运算基本由乘法和加法满足,因此可以适用同态加密算法。
卷积也是一种线性变换,其通过计算卷积核和输入特征图中元素邻域的点积来获取输出的值,通过滑动窗口的方式在每一步中将卷积核滑动一定量来重复该过程。邻域的大小称为窗口大小,滑动的间隔称为步幅。但是本质上来说,卷积所进行的操作仍然脱离不了加法和乘法的范畴,如果将输入和输出看作矩阵,那么卷积完成的运算仍然可以线性的表示为:$\mathbf{Y=WX+B}$ 。
Dropout也是线性变换的类型,Dropout使得我们随机地去掉一些参数参与运算,这是通过逐元素乘以一个0-1随机掩码得到的。BatchNorm是一种自适应的归一化方法,在推理过程中,其实际上同样地等价于矩阵的加法和乘法。
对于这些线性操作而言,无论是同态加密还是混淆电路加密都是较为容易实现的,但是考虑到线性操作相当频繁,因此针对线性的运算开销优化往往是继续推进推理速度的核心,因此需要选择合适的加密方案并进行细致的调整。
非线性部分
神经网络的非线性部分是不可或缺的,其中最重要的非线性部分即激活函数。在每一层的线性推理结束后,我们通过激活函数来引入非线性性。最常见的激活函数即ReLU函数:$f(\mathbf{y}) = [ \max (0,y_i) ]$。对于ReLU函数来说,通常不能直接地进行同态加密,因此往往会选择以混淆电路为基础的安全两方计算方法来进行安全推理。另一种解决方案是,采用其他引入非线性的激活函数,例如 $f(\mathbf{y}) = [y_i^2]$ ,这样可以使得同态加密兼容激活函数,但是对于已经使用了ReLU进行训练的模型来说,可能就面临着改变激活函数重新训练模型的代价。
池化层是神经网络中常见的一种降采样的方式,最常见的分为平均池化和最大池化两种,其中最大池化也是一种非线性的操作。因此对于该部分常见的处理方式也是使用基于混淆电路的安全推理协议。
安全推理的实现和优化
通过前面的介绍我们已经可以大致了解对神经网络进行安全推理的思想,从而大致地构建一个安全推理的雏形。一个比较容易得到的方案是,将深度学习模型的每层的输入结构公布给客户端,然后服务端的每层推理都针对性的应用同态加密或混淆电路方法,并且每层都和客户端进行中间结果的交互,在其中只需引入秘密共享的思想,即可以保证中间结果由服务端和客户端共同享有,任何单独一方都不能获知推理的中间结果。这一方案也是绝大多数研究所重点关注的方案,并且在这一思想的指导下进行了多种计算优化。
但是还存在着另一种可能,即在全同态加密的基础上进行安全推理,从而不需要中间结果的交互,服务端直接接收密文并独立完成全部推理过程。这一方案则需要深度学习模型在非线性部分做出让步,比如规避ReLU激活函数和最大池化等。但是这一方案的优势是,服务端的模型结构是不公开的,从而提升了对模型的保护。
在本节中,我们整理了这两种安全推理的思路,并选取了在推理优化中做出重要贡献的一些工作进行介绍。
部分同态加密和混淆电路结合
使用部分同态加密和混淆电路相结合是诸多学者重点关注的方案。该方案可以让服务端和客户端交互地逐层完成密文推理,而不泄漏双方的隐私信息。在早期的SecureML模型\中即对这种方案进行了阐述,而在2017年的工作MiniONN中则对这一思想进行了进一步的细化。
具体来说,MiniONN中对于一个线性层的推理实现过程大致如下:
-
首先,每层的输入由两方各自持有一部分:$\mathbf{x}^S$ 和 $\mathbf{x}^C$ (其中S表示服务端,C表示客户端),并且 $\mathbf{x} = \mathbf{x}^S + \mathbf{x}^C$。
-
服务端将该层的权重 $\mathbf{W}$ 进行同态加密得到 $\widetilde{\mathbf{W}}$,并将其发送给客户端。由于加密,客户端无法得知服务端的真实权重参数值。
-
客户端生成随机数 $\mathbf{y}^C$ ,并进行同态计算: $\mathbf{\widetilde{y_0}} = \mathbf{\widetilde{W}} \otimes \mathbf{x}^C \ominus \mathbf{y}^C$ ,将结果发给服务端,其中 $\otimes$ 表示同态乘法,$\ominus$ 表示同态减法。
-
服务端解密 $\mathbf{\widetilde{y_0}}$ 得到 $\mathbf{y_0}$ ,计算 $\mathbf{y_1} = \mathbf{W} \mathbf{x}^S$,得到 $\mathbf{y}^S = \mathbf{y_0 + y_1 + b}$。由于同态计算的性质, $\mathbf{y_0} = \mathbf{W}\mathbf{x}^C - \mathbf{y}^C$,故而 $\mathbf{y}^S = \mathbf{W}\mathbf{x}^C - \mathbf{y}^C + \mathbf{W} \mathbf{x}^S + \mathbf{b}$,即 $\mathbf{y} = \mathbf{y}^S + \mathbf{y}^C$。从而双方各自保留了一部分中间结果,用于下一步推理。
如此我们可以看到,对于每一层的中间结果,服务端和客户端都各自持有一个部分,并且能够借助同态加密合作完成推理过程。对于卷积等运算,MiniONN首先将其转化为矩阵乘法和加法的形式,再借助上面的流程进行计算。而对于非线性部分,MiniONN借助混淆电路的方法,由双方共同参与非线性函数的计算,从而得到计算结果。而且,在应用这一方法的过程中,我们可以看到客户端和服务端在同态计算时的参与角色是可以互换的,也即可以由客户端同态加密 $\mathbf{x}^C$ ,由服务端进行同态运算并减去随机数 $\mathbf{y}^S$ ,最后由客户端完成解密得到 $\mathbf{y}^C$。
特别地,我们可以注意到,针对服务端的权重 $\mathbf{W}$ ,客户端输入 $\mathbf{x}^C$,客户端输出 $\mathbf{y}^C$ 三者而言,$\mathbf{x}^C$ 是上一层推理生成的随机数,$\mathbf{y}^C$ 是本轮推理生成的随机数,$\mathbf{W}$ 是预先训练好的权重,三者都不依赖网络推理的输入就可以提前生成。因此我们可以预先把每层的这些加密参数计算好,当有网络输入时直接进行推理即可,这就能极大加快推理的速度。
但是上述方法的时间开销仍然是巨大的,这是因为对数据的加密、同态运算和解密等过程都需要耗费相当大的运算量。这些额外的运算是由加密的安全性所天然导致的。因此许多研究人员开始逐渐挖掘加密过程中的一些特性,并开始探索SIMD,即单指令多数据方式,可以将多条数据同时打包到一起,并同时参与运算,这样可以实现并行处理,从而加快运算过程。
在探索SIMD方式中做出阶段性成果的是2018年的Gazelle模型,该模型选择由客户端对输入数据进行打包的同态加密,由服务端进行同态运算。但是对于简单的打包,从打包后的密文中提取运算结果的过程仍然是耗费很大开销的,因此Gazelle提出了一种新的运算方式,用于解决打包过程中产生的问题,具体思想如下图所示。
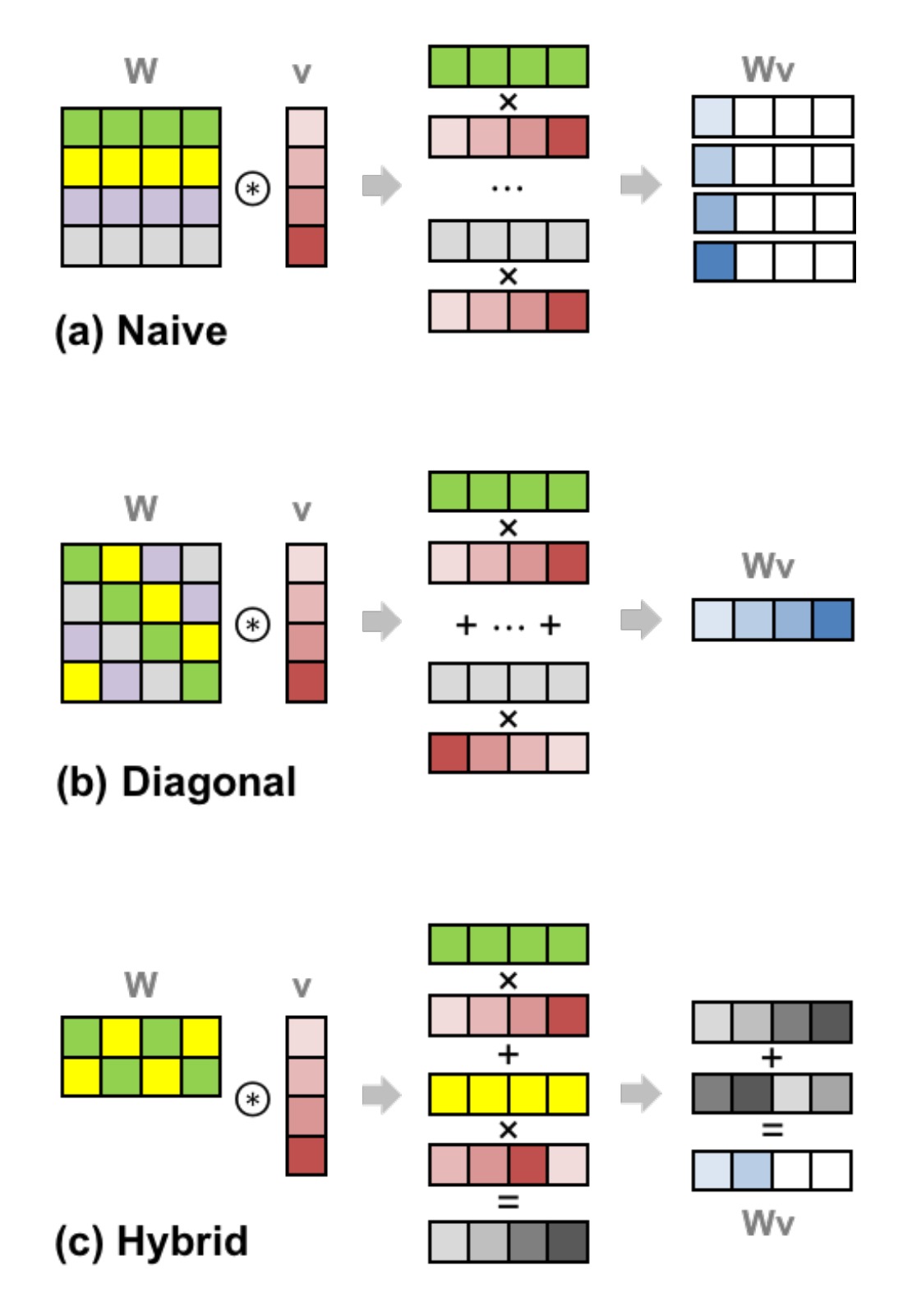
图中的列向量 $\mathbf{v}$ 具有4个元素,我们可以理解为将其打包到4个格子里面并一起加密,然后我们将其复制4份,使得 $\mathbf{v}$ 会和 $\mathbf{W}$ 进行逐行的逐位乘法(如图(a)所示),这样会得到4行运算后的结果。然后我们需要把每一行中的元素都加到最左边的元素上,以完成求和的过程。
请注意,我们不能随意地将打包中的元素提取出来,直接和权重参数进行运算,这是同态加密的打包方案所不支持的。同态加密的打包方案仅仅支持逐位的加法、乘法和密文的旋转,旋转即置换密文各个元素在打包中的排列顺序。这里把每一行的结果相加的过程,实际上使用的就是旋转操作,我们将每一行的元素旋转置换位置,再把它们彼此相加,从而得到的结果就是该行中所有元素求和的结果。求和以后得到的结果即如图(a)中蓝色块的分布所示,我们还需要对每行中剩余位置清零,然后旋转蓝色块到对应的位置,最后相加才能够得到一个打包好的运算结果。
由于同态运算中的旋转操作是非常昂贵的,这样的打包并不能使得计算效率有明显的提升。因此Gazelle提出了对角线的运算方案(如图(b)所示),即事先旋转打包后的列向量 $\mathbf{v}$ ,并且将矩阵的参数顺序也做出对应地调整,使得对应位置仍然参与对应的运算,但是无需后面的旋转而可以直接求和。对于参数矩阵的高宽不等的情况,Gazelle认为应当采用一种混合对角线的计算方法(如图(c)所示),使得子矩阵仍然可以通过对角线计算来优化计算过程。
事实上,Gazelle对于卷积层也做了类似的努力,并且同样地通过调整计算顺序来极大降低了旋转操作的次数,从而使得时间开销大幅减少。随着SIMD方法的成功应用,后续的诸多工作都在Gazelle的基础上展开,使得SIMD进一步得到优化。但是近年来,随着SIMD的性能挖掘逐渐困难,研究人员开始探索新的加快计算效率的方法,2022年的工作Cheetah放弃了SIMD,转而通过多项式运算的方式,来进行安全推理的运算优化,这也是目前公认能够达到性能最优的解决方案。

Cheetah认为神经网络中的线性运算都由逐项乘积后求和两个步骤组成,而如果将参与运算的两方表示在多项式环上,那么这些线性运算的结果实际相当于多项式运算的系数。如上图所示,以一个简单的矩阵向量乘法为例,我们将列向量 $\mathbf{v}$ 的参数正序排布,将矩阵 $\mathbf{W}$ 的参数逐行倒序排布,分别用多项式的形式表示,然后我们进行两个多项式的乘法运算,由于逐项相乘之后相同幂次的系数会相加,因此这时矩阵乘法的结果就已经包含在多项式的系数中。Cheetah通过引入多项式环的同态加密,利用多项式乘法的经典快速运算方法,规避了SIMD中旋转操作的高昂代价,使得时间开销得到进一步下降。
这一系列的工作中,优化的核心往往放到同态加密部分,这是因为在神经网络中线性层参与的运算量要明显的更多。但是这并不意味着针对非线性层的优化不重要,事实上,上述工作中Gazelle和Cheetah也都分别对混淆电路中的运算协议进行了优化,这些优化也为降低网络推理的时间开销做出了贡献。
全同态加密
使用全同态加密的方法,让客户端上传一份加密数据后就完全由服务端进行全部推理过程,最后将结果告知客户端,这一想法的新颖性在于规避了服务端与客户端对中间结果的交互所造成的信息泄漏风险。在2021年的工作中,首次比较全面的建立起了基于全同态加密的深度神经网络的推理过程。在该模型中,我们调整神经网络的结构,为其插入全同态加密的自举操作,使得整个加密计算的流程无需客户端的参与,最终仍然能够得到正确结果。
然而,全同态加密的方案相对于4.1中部分同态的方案往往带来更高的开销,这是因为全同态加密方案往往基于SIMD的打包方法。而在这里客户端一旦打包之后,是不会再和服务端进行交互的,因此服务端就无法对密文的结构进行调整。由于神经网络中常常出现降采样等操作,初始打包的密文无法对信息密度进行调整,就导致了随着网络的推理,打包的密文的信息密度逐渐降低,使得SIMD无法发挥其应有的作用。
我们可以举一个例子来说明上述问题,假如神经网络输入的特征图为 $8\times 8$ 矩阵,我们应用SIMD将这个矩阵打包到一起,当经过步长为2的卷积层后,输出特征图的大小将变为 $4\times 4$ ,由于我们需要维持初始的打包结构,因此这个包裹中的64个元素只有16个元素是有意义的,如果后面还有继续的降采样的话,该包裹中的信息密度还会进一步降低。
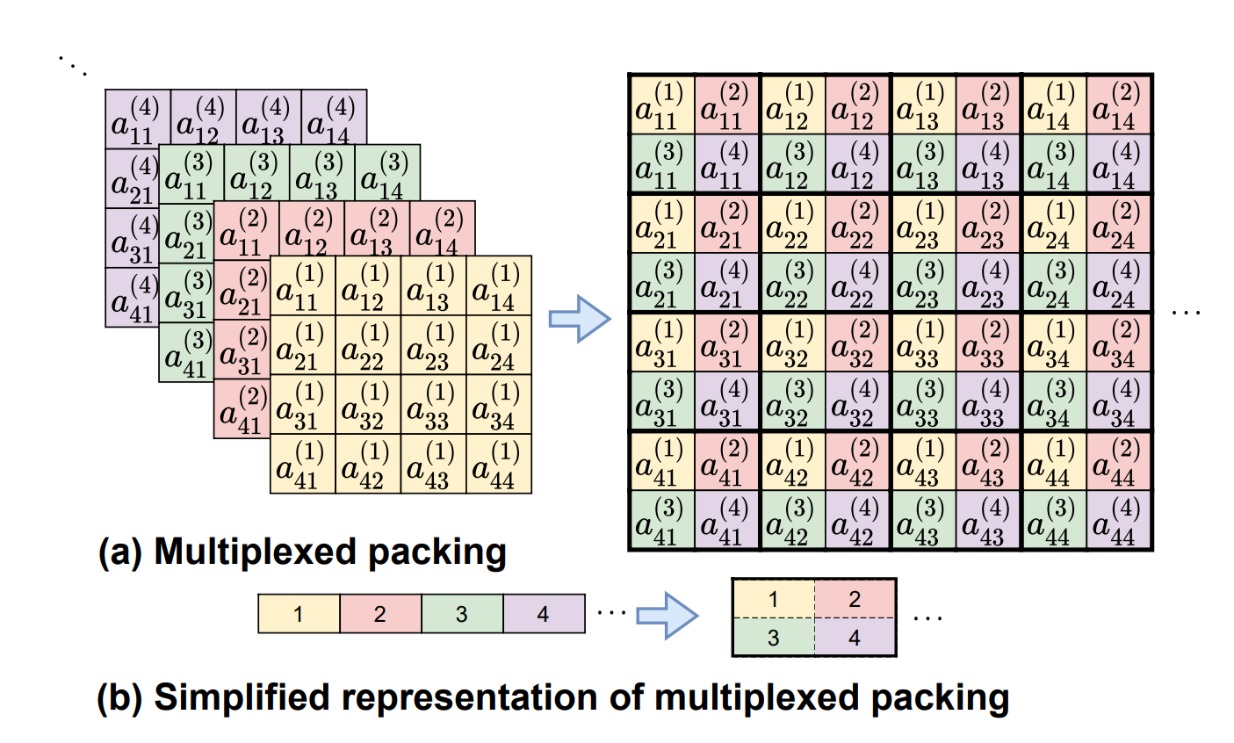
2022年有研究人员注意到了该问题,提出了针对全同态加密方案的多通道填充优化方式,其基本思想如上图所示。针对在运算过程中信息密度逐渐降低的问题,该工作认为可以将空余的元素利用起来。由于卷积神经网络往往是多通道的,因此可以将不同通道的元素输出都填充到同一个包裹中。具体来说,图中的64个元素经过步长为2的降采样,只有16个元素代表了该通道的输出结果,那么我们就将另外3个输出通道的48元素都填充到这个包裹中,使得该包裹中的信息密度不会降低,从而原本的4个包裹变成了1个包裹,这样降低了运算的成本。
这样的多通道优化填充能够明显的解决信息密度下降的问题,但是由于填充过程中额外会产生很多的旋转操作,因此在效率上仍然有提升的空间。2023年有研究人员基于此提出了名为HyPHEN的方案,该方案混合了多种填充和运算顺序,在运算的处理上更加精细,也让我们看到了全同态加密方案能达到的更优效果。
我们在前节中看到,部分同态加密的方案中提出用多项式运算来代替SIMD,得到了更优的效果。但是多项式方法是很难应用到全同态加密中的,这是因为全同态加密中的激活函数需要逐元素的运算,即使是采用平方激活函数,仍然是不能通过多项式的系数来表达的。因此这限制了多项式方法在全同态加密上的应用。但是结合多项式方案的全同态加密仍然是未来值得研究的一个方向,或许在不久的将来就能够出现更加出色的优化方法。
总结
隐私保护的深度学习是大家共同关注的重要问题,随着深度学习模型规模的增大和应用的拓展,对安全性的要求日益增加。目前我们所看到的方法中,大多以同态加密和安全两方计算为代表,并结合神经网络的层次特性进行针对性的处理。许多工作会结合一些计算优化方法,来提高推理的性能,这也极大提高了安全推理的应用可能。但是目前这些方法能达到的性能还不足以完全地提供大型的云端服务,其时间开销距离真实的应用场景还有不小的差距,要弥补这些差距的代价是较为高昂的硬件加速成本。不过随着新的优化方法的提出,结合一些硬件加速方式,在一些涉及重要隐私的安全推理问题上,我们已经可以看到其应用的曙光。并且随着更多优化方法的出现,安全推理的价值将能够更加凸显。
参考文献
-
ElGamal, Taher. “A public key cryptosystem and a signature scheme based on discrete logarithms.” IEEE transactions on information theory 31.4 (1985): 469-472.
-
Paillier, Pascal. “Public-key cryptosystems based on composite degree residuosity classes.” Advances in Cryptology—EUROCRYPT’99: International Conference on the Theory and Application of Cryptographic Techniques Prague, Czech Republic, May 2–6, 1999 Proceedings 18. Springer Berlin Heidelberg, 1999.
-
Yao, Andrew Chi-Chih. “How to generate and exchange secrets.” 27th annual symposium on foundations of computer science (Sfcs 1986). IEEE, 1986.
-
Gentry, Craig. “Fully homomorphic encryption using ideal lattices.” Proceedings of the forty-first annual ACM symposium on Theory of computing. 2009.
-
Mohassel, Payman, and Yupeng Zhang. “Secureml: A system for scalable privacy-preserving machine learning.” 2017 IEEE symposium on security and privacy (SP). IEEE, 2017.
-
Liu, Jian, et al. “Oblivious neural network predictions via minionn transformations.” Proceedings of the 2017 ACM SIGSAC conference on computer and communications security. 2017.
-
Juvekar, Chiraag, Vinod Vaikuntanathan, and Anantha Chandrakasan. “{GAZELLE}: A low latency framework for secure neural network inference.” 27th {USENIX} Security Symposium ({USENIX} Security 18). 2018.
-
Kumar, Nishant, et al. “Cryptflow: Secure tensorflow inference.” 2020 IEEE Symposium on Security and Privacy (SP). IEEE, 2020.
-
Rathee, Deevashwer, et al. “CrypTFlow2: Practical 2-party secure inference.” Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security. 2020.
-
Huang, Zhicong, et al. “Cheetah: Lean and Fast Secure {Two-Party} Deep Neural Network Inference.” 31st USENIX Security Symposium (USENIX Security 22). 2022.
-
Lee, Joon-Woo, et al. “Privacy-preserving machine learning with fully homomorphic encryption for deep neural network.” IEEE Access 10 (2022): 30039-30054.
-
Lee, Eunsang, et al. “Low-complexity deep convolutional neural networks on fully homomorphic encryption using multiplexed parallel convolutions.” International Conference on Machine Learning. PMLR, 2022.
-
Kim, Donghwan, et al. “HyPHEN: A Hybrid Packing Method and Optimizations for Homomorphic Encryption-Based Neural Networks.” arXiv preprint arXiv:2302.02407 (2023).