传统对称密钥密码
代换密码
首先介绍单码代换密码,这些密码的特点是建立26个字母到26个字母的一一映射,密文用新字母表示明文的旧字母
加法密码
我们将字母 A ~ Z 对应到 0 ~25 ,那么加法密码的加密解密过程可以表示为:
\[C = (P+k)\mod 26 \\ P = (C-k) \mod 26\]历史上,加法密码被称为移位密码,因为加密算法可以认为是向下/向上移动密钥字符,到达字母表的开头和结尾之后再返回来。k = 3 的密码被称为 Caesar 密码,即 a 的密文为 d,b 的密文为 e,以此类推,Caesar 曾利用该密码与其官员通信。
乘法密码
乘法密码同样是基于数学,将字母 A ~ Z 对应到 0 ~25,然后加密解密过程可以表示为:
\[C=(P \times k) \mod 26 \\ P=(C \times k^{-1}) \mod 26\]请注意,在 $\mathbb{Z}_{26}$ 中不是所有的元素都有逆元,因此 $k$ 的取值范围并不是 1~26,而只能是那些有逆元的元素:
\[k \in \mathbb{Z}_{26}^{\ast} = \{1,3,5,7,9,11,15,17,19,21,23,25 \}\]仿射密码
仿射密码是加法密码和乘法密码的结合: \(C=(P \times k_1 + k_2) \mod 26 \\ P=((C-k_2) \times k_1^{-1}) \mod 26\) 仿射密码的密钥由 $(k_1,k_2)$ 组成,仿射密码能够形成更多的代换组合。
单表密码
利用一张字母映射表(密码本)建立明文与密文之间的一一映射。
在单表代换密码中,字母表(密码本)中的字母顺序可以被任意打乱。26个字母的排列方法总共有 $26!$ ,大约是$4×10^{26}$,在抵抗蛮力攻击能力方面有所提高。
例如以下明文和密文的密码本:
ABCDEFGHIJKLMNOPQRSTUVWXYZ
QWERTYUIOPASDFGHJKLZXCVBNM
下面是多码代换密码,这些密码的特点明文字符和密文字符的关系并不是自始至终一对一的,明文字符在不同位置的出现也许会有不同的代换
自动密钥密码
选一个字母做初始密钥,之后每一个字母的新密钥是上一个字母的明文值。
例如:初始密钥 m
| 明文流 | a | t | t | a | c | k | i | s | t | o | d | a | y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 密钥流 | m | a | t | t | a | c | k | i | s | t | o | d | a |
| 密文流 | m | t | m | t | c | m | s | a | l | h | r | d | y |
但是该密码的密钥域较小,容易受到蛮力攻击。
PlayFair密码
一战中英军使用的密码。密钥是一个5X5的字母方阵,把26个字母填入其中(i, j 填在同一格中)。一种可能的排列如下所示:
\[\left[ \begin{array}{c} L & G & D & B & A \\ Q & M & H & E & C \\ U & R & N & I/J & F \\ X & V & S & O & K \\ Z & Y & W & T & P \\ \end{array} \right]\]加密之前要先做处理:将明文2个字母组成一对,若两字母相同,嵌入一个伪字母,若最后是奇数,在结尾嵌入一个伪字母,这样保证明文字母个数是偶数个,相邻两两结对,而且每对的两个字母不同。
加密时每两个字母一起加密,这两个字母在加密时按照如下规则生成密文:
- 如果两个字母位于同一行,那么每个字母的加密字符就是同一行中右侧的下一个字母
- 如果位于同一列,那么每个字母的加密字符就是同一列中下面的字母
- 如果位于对角,那么每个字母的加密字符就是处于自己所在行和另个字母所在列的字母
例如对于 hello 进行加密,首先对 hello 进行处理,在两个 l 之间插入分割的 x ,得到 he, lx, lo
\[he \rarr EC \ \ lx \rarr QZ \ \ lo \rarr BX \\ 明文:hello \ \ \ 密文:ECQZBX\]我们可以发现在这个过程中,密钥流和密码流是相同的,密文同时就是解密的密钥
Vigenere密码
Vigenere密码中的密钥流是一个长度为 m 的起始密钥流的重复,其中 m 小于等于26。
\[P=P_1P_2P_3... \\ C=C_1C_2C_3... \\ K=[(k_1,k_2,...,k_m),(k_1,k_2,...,k_m),...] \\ \\ C_i = (P_i + k_i) \mod 26 \\ P_i = (C_i - k_i) \mod 26\]Vigenere密码的不同之处在于,其密钥流不依赖于明文字符,只依赖于明文字符的位置。换言之,密钥流是独立于明文字符选取的。
例如,密钥 K=PASCAL
| P | s | h | e | i | s | l | i | s | t | e | n |
|---|---|---|---|---|---|---|---|---|---|---|---|
| K | p | a | s | c | a | l | p | a | s | c | a |
| C | h | h | w | k | s | w | x | s | l | g | n |
Hill密码
Hill也被称为矩阵密码,不同于之前的流密码,它属于分组密码的一种。具体来说加密方法如下:
密钥: $K = (k_{ij})_{m\times m}$ 矩阵 K mod 26 可逆
明文分为长度为 m 的分组,共 r 组(即矩阵 $P_{r\times m}$ r 行 m 列 )
\[C = P \cdot K \mod 26 \\ P = C \cdot K^{-1} \mod 26\]一次一密密码
每发送一次信息,改变一次密钥。
密钥完全随机生成,密钥长度固定。
一次一密密码是一种理想密码,但是商业性地实现这种密码几乎是不可能的。
换位密码
换位密码是采用移动字母位置的方法进行加密的。它把明文中的字母重新排列,字母本身不变,但位置变了。如:把明文中的字母的顺序倒过来写,然后以固定长度的字母组发送或记录。
无密钥换位
栅栏密码就是无密钥换位的一种,明文分为两行,竖写横读。
如明文:WHAT YOU CAN LEARN FROM THIS BOOK
\[\begin{array}{c} W & A & Y & U & A & L & A & N & R & M & H & S & O & K \\ H & T & O & C & N & E & R & F & O & T & I & B & O & X \end{array}\]表格换位是栅栏密码的一种扩展,如将明文字符分割成为五个一行的分组,排进表格中,横写竖读。
明文:WHAT YOU CAN LEARN FROM THIS BOOK
分组排列为:
\[\begin{array}{c} W & H & A & T & Y \\ O & U & C & A & N \\ L & E & A & R & N \\ F & R & O & M & T \\ H & I & S & B & O \\ O & K & X & X & X \\ \end{array}\]密文则以下面的形式读出:
WOLFHOHUERIKACAOSXTARMBXYNNTOX
有密钥换位
密钥K就是一个指定的置换。
例如:把明文分成5个字母一段。每段都按照密钥指定的置换方式进行换位。
加密密钥 $K=[3\ \ 1\ \ 4\ \ 5\ \ 2]$ 这里的1-5表示的是原始排列的索引,即新排列的第一个字母是原始的第3个字母,以此类推
明文:Enemy attacks tonight
| Enemy | attac | kston | ightz |
|---|---|---|---|
| EEMYN | TAACT | TKONS | HITZG |
用矩阵乘法表示换位:
\[K = [3 \ \ 1 \ \ 4 \ \ 5 \ \ 2] \\ K = \left[ \begin{array}{c} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \end{array} \right]\]也即:
\[\left[ \begin{array}{c} e & n & e & m & y \\ a & t & t & a & c \\ k & s & t & o & n \\ i & g & h & t & z \\ \end{array} \right] \times \left[ \begin{array}{c} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \end{array} \right] = \left[ \begin{array}{c} e & e & m & y & n \\ t & a & a & c & t \\ t & k & o & n & s \\ h & i & t & z & g \\ \end{array} \right]\]组合两种方法
更现代的方法是组合两种方法,加密通过三步来完成:
- 文本逐行写入表中
- 通过每行内的列重排实现字符的转换
- 对新表逐列阅读
解密则相反:
- 文本逐列写入表中
- 通过每行内的列重排实现字符逆向转换
- 对新表逐行阅读
上述加密过程可以视为经过了一个换位盒。
更进一步地,上述步骤可以重复多个循环,即让密文通过多个换位盒,每个换位盒的置换密钥可以不同。
现代对称密钥密码
现代对称密码的加密技术
基本加密方法——代换(换字盒)和置乱(换位盒)
换位盒
换位盒分为直接换位盒,压缩换位盒和扩展换位盒。直接换位盒即如前所述的置换操作,压缩换位盒和扩展换位盒分别如图所示。
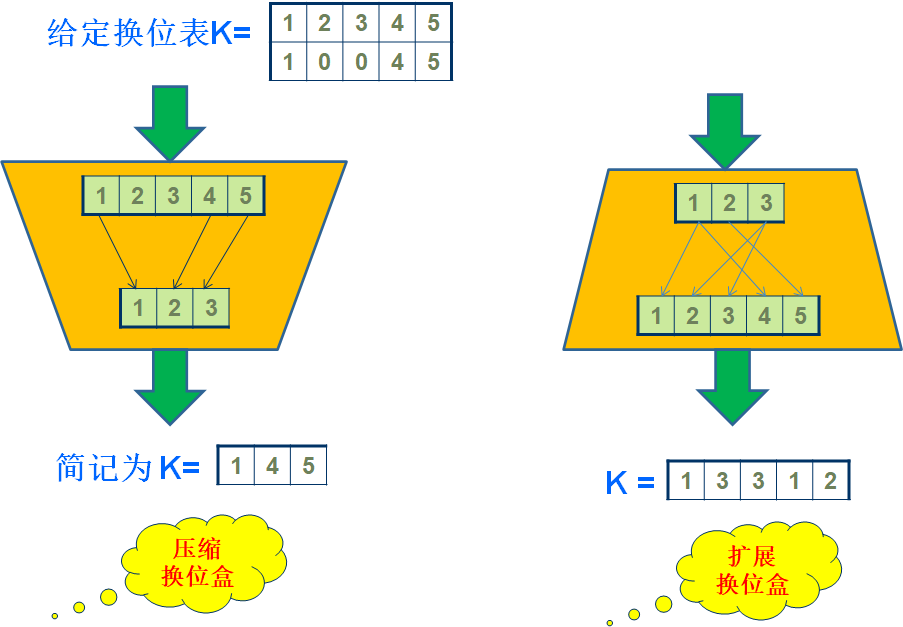
直接换位盒是可逆的,但是压缩换位盒和扩展换位盒没有逆。压缩换位盒并不是扩展换位盒的逆,反之亦然。
换字盒
换字盒的思想来源于代换密码,然而一个换字盒的输入和输出数目可以是不同的。
虽然换字盒可以是有密钥的或者是无密钥的,但是现代分组密码通常使用无密钥换字盒,其中输入到输出的映射是预先设定的。
下表是一个 $3 \times 2$ 换字盒的例子:
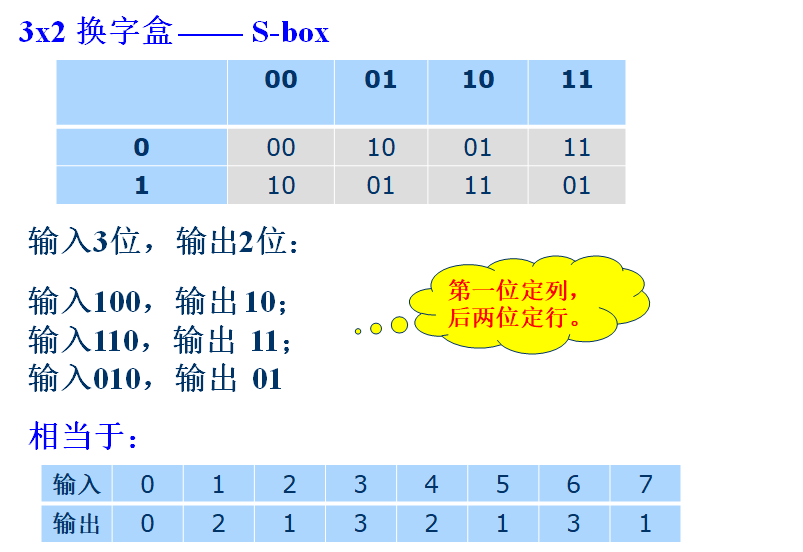
Fistel结构
Fistel设计了一种高明的结构,它让加密和解密算法都有一个不可逆的元,但是加密和解密算法却能够达到互逆的效果。
我们用异或运算来解释这一效果,我们使用一个不可逆函数 $f(K)$。
\[\begin{array}{l} 加密:C_1 = P_1 \oplus f(K) \\ 解密:P_1 = C_1 \oplus f(K) = P_1 \oplus f(K) \oplus f(K)= P_1 \end{array}\]这是一种初级的想法,我们对不可逆函数的输入不能仅仅依赖密钥,我们引入新的表示 $f(R,K)$,$R$ 在加密时表示明文的一部分,在解密时对应密文的一部分。从而这要求了该部分在明文和密文中应当是一致的。一个初步的想法是将明文和密文都分成左右两个长度相等的组,加密解密过程如下图所示。
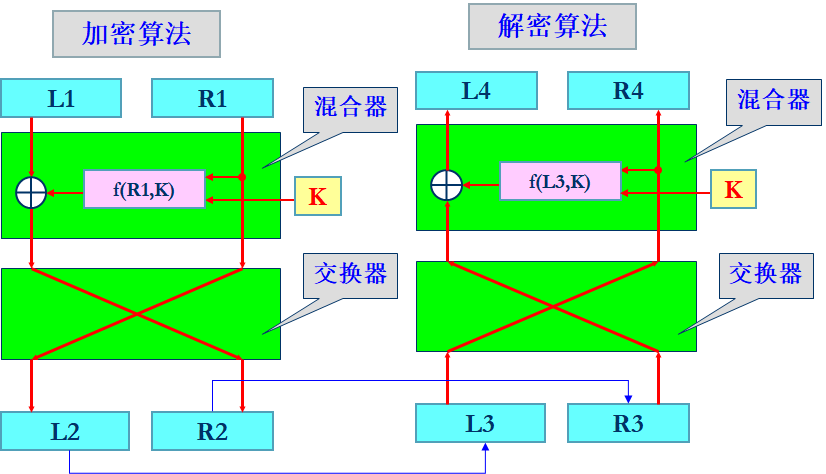
我们认为 $L_3=L_2$ 并且 $R_3=R_2$,加密解密过程如下所示:
\[\begin{array}{l} 加密:L_2 = R_1, \ \ R_2 = L_1 \oplus f(R_1,K) \\ 解密:R_4 = L_3 = L_2 = R_1, \ \ L_4 = R_3\oplus f(L_3,K) = L_2 \oplus f(R_1,K) = L_1 \end{array}\]但是上述设计仍然有一个缺陷,那就是明文的右半部分是直接映射到密文的左半部分的,这就给了拦截破获的可能。一个最直观的改进是将上述过程重复多轮,这样密文的左半部分参与下一轮的加密,这样重复多轮之后就不存在可以轻易破获的可能了。这也是交换器在这一结构中存在的原因。
数据加密标准DES
DES加密算法是一个对称算法,加密和解密用同一算法和密钥。DES加密算法是分组密码( Block cipher),明文分成64位的分组进行加密,输出64位密文,密钥长度64位,其中56位密钥,8位校验位。DES加密算法分为16轮,每轮结构相同,每一轮采用Fistel结构。
DES采用两种最基本的加密思想:
- 扩散(Diffusion):使得明文和密文之间的统计关系尽量复杂
- 混乱(confusion):使得密文的统计特性与密钥的取值之间的关系尽量复杂
DES整体结构
设明文 $M$ 和密文 $K$ 均为由0和1组成的64位的符号串:
\[M = m_1 m_2 ... m_{64} \\ K = k_1 k_2 ... k_{64}\]其中 $k_8,k_{16},k_{24},…,k_{56},k_{64}$ 为奇偶校验码。
DES算法由一系列循环运算(16轮)组成:
\[DES(M) = IP^{-1} \circ T_{16} \circ T_{15} \circ ... \circ T_{2} \circ T_{1} \circ IP(M)\]其中 $IP$ 为初始置换,$IP^{-1}$ 为最终置换,二者互逆,$T_1,…,T_{16}$ 为16轮循环运算。
DES整体结构大致如下图:
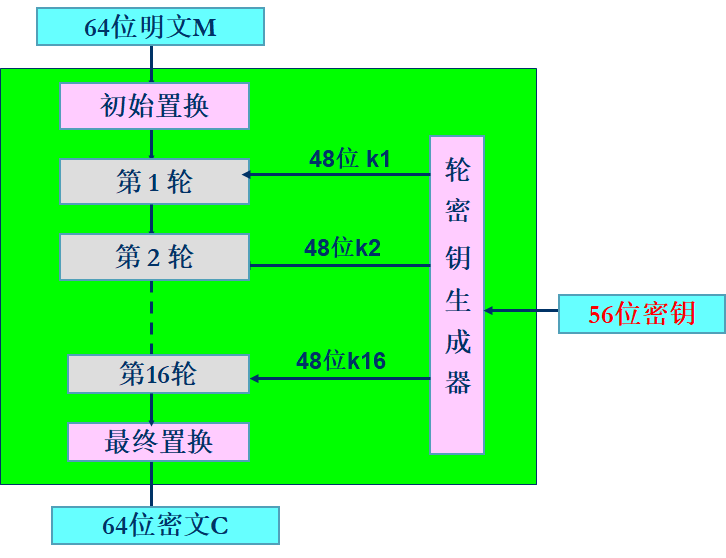
其中,初始置换和最终置换都是64-64位换位盒,中间的每一轮都是Fistel结构。但是在最后一轮的Fistel结构中,DES没有使用交换器,当然这需要解密过程同样的不使用交换器,但是不影响整体的加密效果。
DES函数
DES的重点即在于不可逆部分的函数结构,DES函数 f 的整体结构如下图所示:
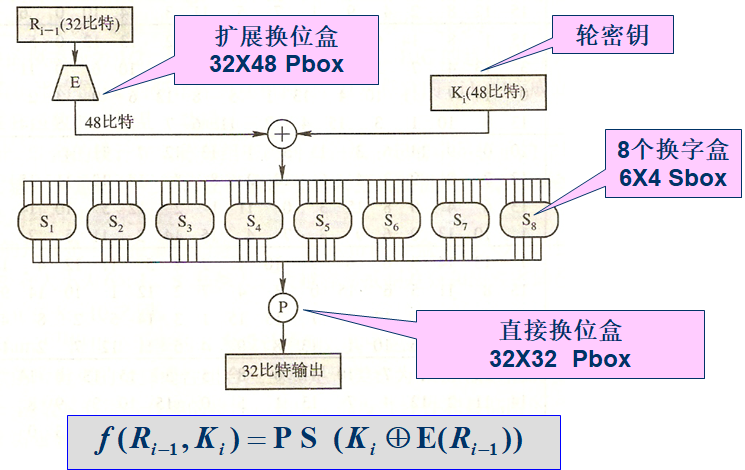
首先是一个32-48扩展换位盒,具体来说这个扩展遵循一个事先确定的规则,即将输入分成8个4比特的部分,然后将每一个4比特的部分扩展成6比特,每个部分输出的2,3,4,5比特对应原始的1,2,3,4比特,而输出的1,6比特则来自于相邻的上一个部分的4比特和下一个部分的1比特,具体规则见下图。

扩展之后,所得到的输出和密钥都是48位的,将二者直接进行异或操作,将异或的结果输入换字盒。换字盒起到真正的混合作用,DES使用了8个换字盒,每一个都是6比特输入和4比特输出。
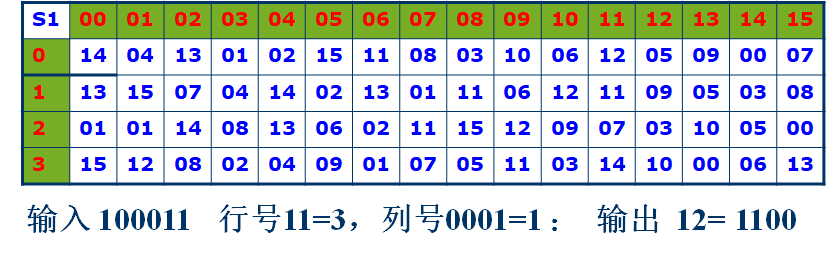
具体来说,每一个换字盒都遵循如下变换,用比特1和比特6组合,确定行号,用剩下的4位确定列号,然后查找表得到4位输出。
密钥生成器
我们的初始密钥只有64位,但我们要为16轮操作均生成密钥,因此我们引入轮密钥生成器,其结构如下图:
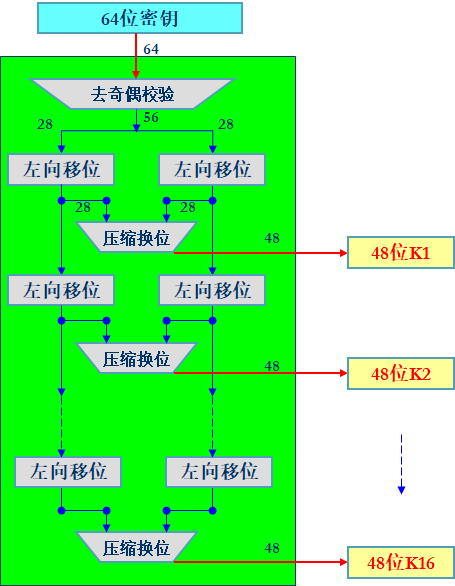
首先我们对64位比特密钥去除奇偶校验位,生成56位密钥,我们将56位密钥分为两组,每组28位,在接下来的加密过程中,每组密钥都进行左向循环移位,每次移位1或2个比特,其结果放到压缩换位盒中输出48位的轮密钥。
高级加密标准AES
AES整体结构
AES是一个非Fistel密码,可以加密和解密128比特的数据分组,它使用10、12或14个轮,密钥的大小分别对应128、192和256比特。不过,由密钥扩展算法创建的轮密钥总是128比特,和明文或密文的大小是相同的。其结构大致如下图。
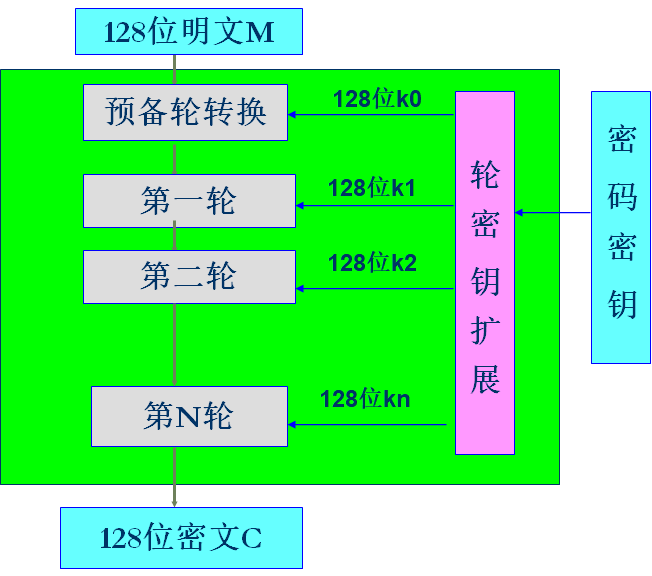
AES轮结构
AES的每个分组由128个比特,即16个字节组成,我们将16个字节的分组表示为4x4的矩阵,称为状态。
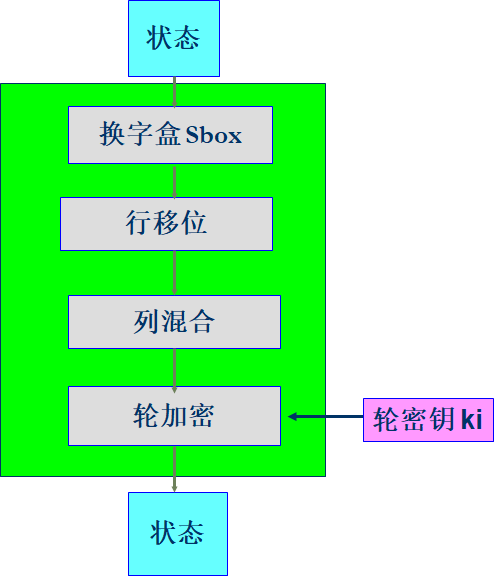
在AES加密中,每一个转换用一个状态,并为下一个转换或下一个轮创建另一个状态。上图为一个普通的轮的结构,中间经历四个转换,分别为换字盒、行移位、列混合、轮加密。在预备轮中仅仅用一个转换,即轮加密,在最后一轮中使用三个转换,没有列混合转换。
换字盒每次对一个字节进行操作,也即对8位比特进行操作。通常可以用前4位表示16进制行号,后4位表示16进制列号,映射到换字表中的相应输出。这也是每一轮中唯一的非线性部分。
换字盒的过程也可以通过有限域 $GF(2^8)$ 上的运算来完成,该有限域带有不可约多项式 $(x^8+x^4+x^3+x+1)$。具体在运行时,将一个字节表示为它在有限域 $GF(2^8)$ 上的乘法逆元,然后将其表示成一个列矩阵,$s^{-1} =s_0s_1s_2…s_7$,然后引入矩阵变换:
\[\left[ \begin{array}{c} y_0 \\ y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ y_6 \\ y_7 \\ \end{array} \right] = \left[ \begin{array}{c} 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{array} \right] \times \left[ \begin{array}{c} x_0 \\ x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \\ \end{array} \right] + \left[ \begin{array}{c} 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \\ \end{array} \right]\]输出 $y = As^{-1} + c$ 作为换字结果。逆换字过程可以表示为 $s^{-1} = A^{-1} (y-c)$。
行移位运算是中间态矩阵中各行的循环左移,移位字节数与行号有关,如下图所示,第0行不移位,之后每行移位依次加一。

列混合变换即是将状态的每一列转换为一个新的列,实际上即让每个状态列和常数矩阵相乘,字节的乘法是在 $GF(2^8)$ 上完成的,加法即异或操作,与此前相同。
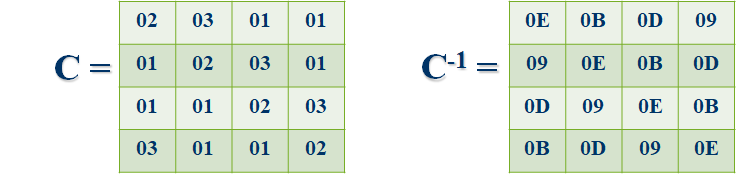
轮加密是每一轮中唯一与密钥相关的操作,它是中间态矩阵各列与密钥字(4字节)的模2加法运算,也即异或运算,故而解密时的逆操作与原操作相同。
AES密钥生成
AES使用长度分别为128, 192, 256位的密钥。利用密钥,产生出轮密钥:共N+1个轮密钥(密钥扩展),轮密钥的长度与分组长度相同,排成相同大小的矩阵。
以AES-128为例,轮密钥创建时以字为单位,共创建 $4\times (N+1)$ 个字,每一个轮密钥都是由4个字构成的,每一轮的密钥用于下一轮密钥的生成。
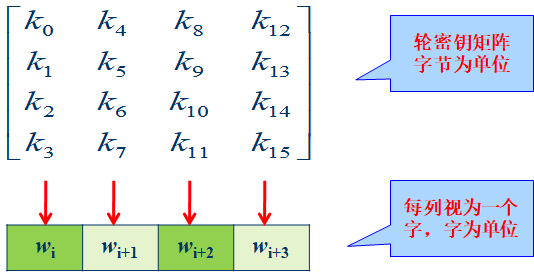
第1个四字是用密码密钥直接制成的,而后面的四字是根据上一轮的字生成的,具体如下图:
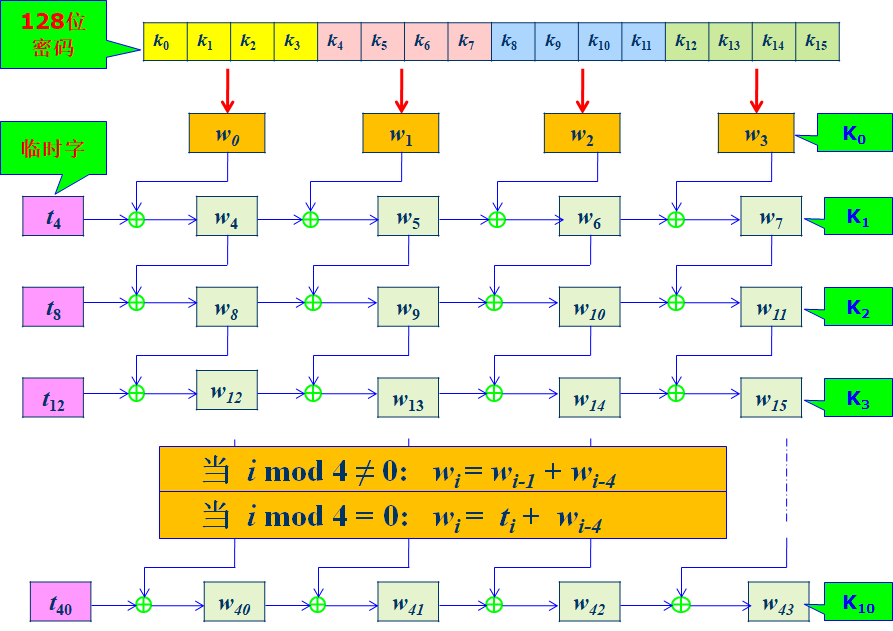
这里的 $t$ 是临时字,它的计算方法如下:
\[t = 字代换(字旋转(w_{i-1})) \oplus RCon_{i/4}\]这里的轮常数RCon是一个四字节的值,是预先指定的。
对于AES-192和AES-256而言,原理基本相似,只不过每一轮生成密钥是分别生成6字或8字。
Camellia加密算法
总体结构
Camellia的外部接口与AES算法相同:明文、密文分组长度位128比特,主密钥长度可以根据性能要求的不同分别选择128、192或256比特。
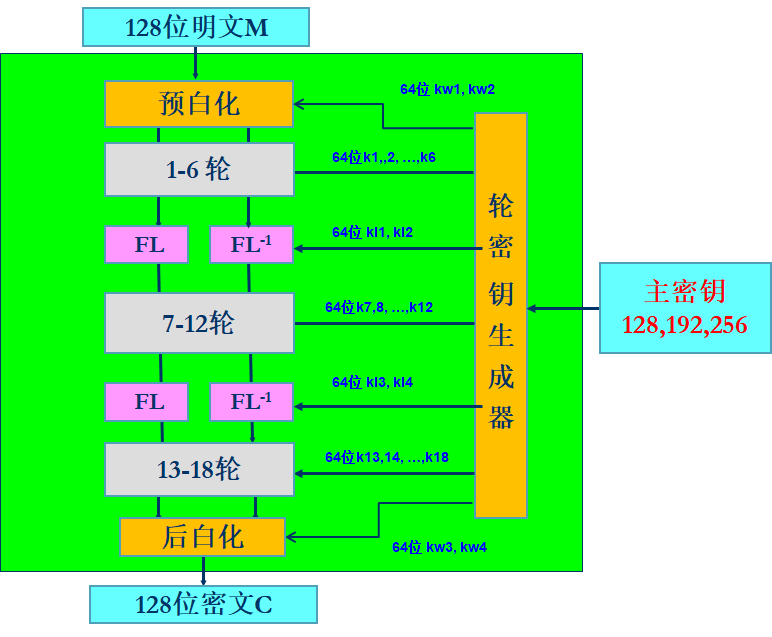
Camellia的结构如上图所示,和AES显著不同的是,Camellia采用了经典的Fistel结构,128位比特明文数据首先与子密钥相异或(称为预白化),然后进行18轮Fistel迭代,其中在第6和第12轮后各嵌入一轮 $FL/FL^{-1}$ 变换层,以打破算法的规律性,最后再与子密钥相异或(称为后白化)然后输出。
当密钥为192/256比特时,在上图的18轮之后需要再嵌入一轮变换层,并再加上6轮Fistel迭代,即总共需要24轮迭代。
F变换
F变换是Camellia算法中最主要的部分,无论是加密、解密还是密钥扩展都要使用该变换。在F变换中,64比特明文和64比特子密钥分别被划分为8个8比特分量,进行以字节为单位的异或运算,然后再相继进行复杂的S变换和P变换。
因此F变换可以描述为子密钥控制下的64比特明文到64比特密文的映射:
\[Z_{(64)}' = F(X_{(64)},k_{i(64)}) = P(S(X_{(64)} \oplus k_{i(64)}))\]F变换整体结构示意图如下:
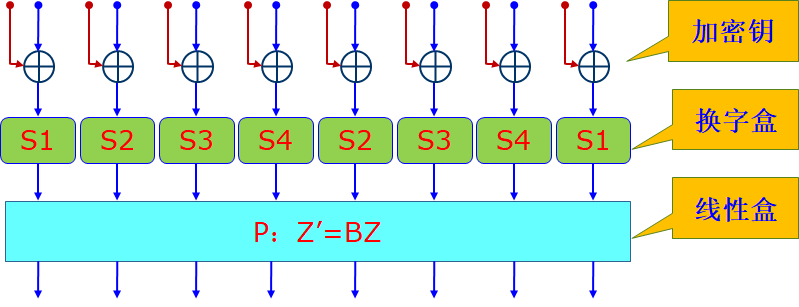
首先是S变换部分,S变换有四个不同的8比特S盒组成,设S盒的8比特输入和输出分别为 $y_{j(8)}$ 和 $z_{j(8)}$ ,则各个S盒的操作可以描述如下:
\[\begin{array}{l} S_1:z_{j(8)} = h(g(f(c_5 \oplus y_{j(8)}))) \oplus 6e \\ S_2:z_{j(8)} = S_1(y_{j(8)}) <<< 1 \\ S_3:z_{j(8)} = S_1(y_{j(8)}) >>> 1 \\ S_4:z_{j(8)} = S_1(y_{j(8)} <<< 1 )\\ \end{array}\]其中,$f$ 和 $h$ 为 $GF(2^8) \rarr GF(2^8)$ 的线性映射,$g$ 为 $GF(2^8) \rarr GF(2^8)$ 的非线性映射。
之后是P变换部分,该部分是一个线性映射,具体操作时是将64比特向量分成8个8比特向量来进行:
\[\left[ \begin{array}{c} z_{8(8)}' \\ z_{7(8)}' \\ z_{6(8)}' \\ z_{5(8)}' \\ z_{4(8)}' \\ z_{3(8)}' \\ z_{2(8)}' \\ z_{1(8)}' \\ \end{array} \right] = \left[ \begin{array}{c} 0 & 1 & 1 & 1 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1 \\ \end{array} \right] \left[ \begin{array}{c} z_{8(8)} \\ z_{7(8)} \\ z_{6(8)} \\ z_{5(8)} \\ z_{4(8)} \\ z_{3(8)} \\ z_{2(8)} \\ z_{1(8)} \\ \end{array} \right]\]式中的加法运算为模2加法,例如:
\[z_{8(8)}' = z_{7(8)} \oplus z_{6(8)} \oplus z_{5(8)} \oplus z_{4(8)} \oplus z_{1(8)}\]$FL$ 和 $FL^{-1}$ 变换
$FL$ 和 $FL^{-1}$ 变换如下图所示:
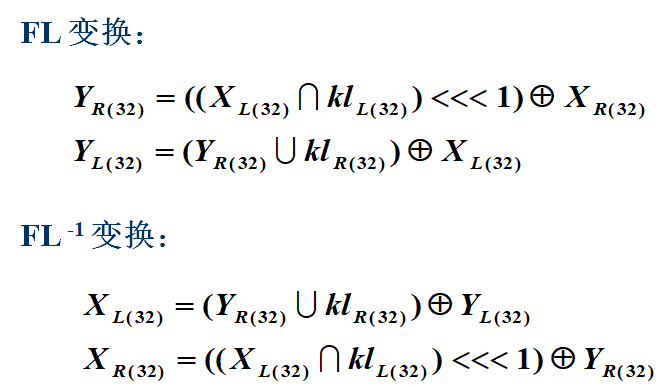
子密钥生成
Camellia算法共需要三种64位的子密钥:
- 预白化和后白化密钥:$kw_{t}$
- Fistel迭代轮密钥:$k_u$
- FL变换密钥:$kl_{v}$
| 主密钥K位数 | t的取值 | u的取值 | v的取值 |
|---|---|---|---|
| 128 | 1,2,3,4 | 1,2,3,…,18 | 1,2,3,4 |
| 192,256 | 1,2,3,4 | 1,2,3,…,24 | 1,2,3,4,5,6 |
首先用主密钥生成两个128位中间密钥:$K_{A(128)}$ 和 $K_{B(128)}$。
利用4个变量,$K_{L(128)}$、$K_{R(128)}$、$K_{A(128)}$ 和 $K_{B(128)}$,进行循环左移位操作即可生成三种子密钥。
应用现代对称密钥密码的加密
在实际应用中,要加密的文本大小可变,长度也可能远远大于64位或128位。任意长度的文本该怎样加密?我们下面列举五种操作模式。
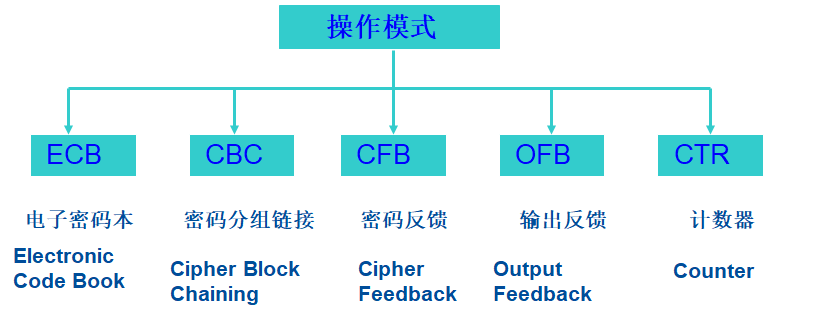
电子密码本(ECB)
最简单的模式即电子密码本模式,把文件分成n比特(通常为64位或128位)的 N 个分组。所有分组都用同一个密码 K 、用相同方法加密。
\[加密:C_i = E_{K} (P_i) \\ 解密:P_i = D_{K} (C_i)\]假如密钥域有 $K$ 位,也即有 $2^K$ 种密钥的可能,而输入明文则可能有 $2^{n}$ 种可能。我们可以预先编辑 $2^K$ 个密码本,每一个都对应一个密钥,每一个密码本都记录了 $2^n$ 个条目,这样我们可以通过直接查询的方式进行加密和解密,所以我们把这种模式称为电子密码本。当然,如果 $K$ 和 $n$ 很大,那么密码本就会过于庞大了。
安全性:
- 分组存在明显对应关系:明文相同的分组其密文分组也相同
- 各分组之间独立:如果知道某一分组传送特定信息,可以用以前拦截的分组信息替代该的分组
- 各分组之间加密方式相同:如果采用蛮力攻击,只需对一个组进行解密,其他组自然也被破解。
- 传输错误的影响:传输中密文若有一位传错,解密时会对本组的很多位产生影响,但不会殃及其他分组。
密码分组链接(CBC)
把文件分成64位或128位的 N 个分组,每一分组先与前密文作异或,然后再加密。第一个分组与初始向量(IV)作异或,发送方和接收方都要同意一个预先确定的初始向量。
\[\begin{array}{l} 加密:\\ C_0 = IV \\ C_i = E_K (P_i \oplus C_{i-1}) \\ 解密:\\ C_0 = IV \\ P_i = D_K (C_i) \oplus C_{i-1} \end{array}\]安全性:
- 分组存在相互关联:前一组的密文会影响下一组的密文,明文相同的分组,其密文分组不一定相同
- 如果前m个分组相同,且IV也相同,则前m个分组的密文也相同
- 攻击者可以在密文流的末尾增加一些密文分组
- 传输错误的影响:传输中若密文有一位传错,解密时会对本组的很多位明文产生影响,还会殃及下一个分组的解密。若第 j 组的密文有一位出错,只会对第 j+1 组相应的同一位置的解密产生影响。对再后面的分组没有影响,单个错误可以自我恢复。
密码反馈(CFB)
在密码反馈中,使用DES或AES并不是为了对明文进行直接的加密,而是为了对大小为 m 的移位寄存器 S 的内容进行加密或解密。每次加密的大小也不一定为64或128,而是一个双方选定的 r 值。移位寄存器最开始为双方选定的初始向量IV,每次加密时对移位寄存器的输出结果加密,取前 r 位与明文异或得到密文传输给对方,然后移位寄存器左移r位,最右边的r比特用密文C填满,这样等待下一次加密。用 $P_i$,$C_i$ 和 $S_i$ 分别表示一次加密时的明文、密文和移位寄存器值,则可以将加密和解密过程表示如下:
\[加密:C_i = P_i \oplus SelectLeft_r \{E_K [ShiftLeft_r(S_{i-1}) | C_{i-1}] \} \\ 解密:P_i = C_i \oplus SelectLeft_r \{E_K [ShiftLeft_r(S_{i-1}) | C_{i-1}] \}\]CFB的整体流程如下图所示:
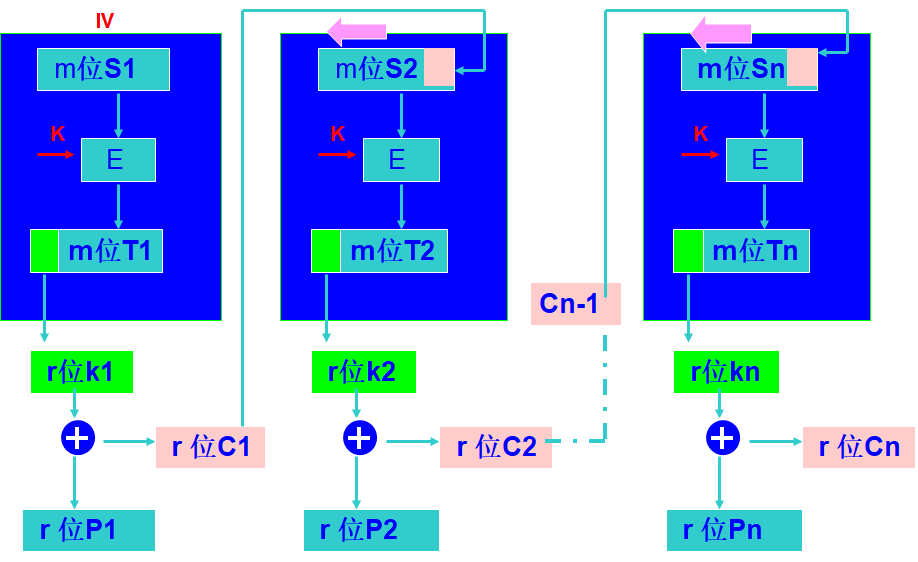
CFB中每次加密的数据量可以很小(如r=8),并且不需要填充。而且CFB本质上是流密码,不需要等到一个大的数据分组(64或128比特)才开始加密。
安全性:
- 分组存在相互关联:前一组的也密文会影响下一组的密钥,明文相同的分组,其密文分组不一定相同
- 不保留分组层
- 攻击者可以在密文流的末尾增加一些密文分组
- 传输错误的影响:传输中若密文 $C_i$ 有一位传错,会对明文 $P_i$ 的同一位位置产生影响。密文 $C_i$ 同时会反馈到下一个分组的移位寄存器,进而影响后面各组的密码,因此对后面个分组的明文都有影响,影响程度远大于CBC。
输出反馈(OFB)
OFB和CFB非常相似,区别仅仅在于填充移位寄存器的右边r位时,OFB不采用密文来填充,而采用上一轮移位寄存器加密过的输出值来填充。这样能够保证解密时,即使上一轮密文在传输过程中出现错误,仍然不会影响后面的解密过程。
安全性:
- 本质上是同步流密钥,密钥流独立于明文和密文,但由于密钥反馈的机制,密钥分组是相互关联的。
- 不保留分组层
- 传输错误的影响:$C_i$ 有一位传错,只会对明文 $P_i$ 的同一位置产生影响。这就避免了错误的传播。 适合带噪信道上的数据传输(比如卫星通讯)
计数器(CTR)模式
计数器模式同样是不直接加密明文,而是通过加密计数器的值,将其和明文进行异或,来达到加密的目的。在计数器模式中不存在反馈,密钥流中的伪随机是通过计数器获得的,一个n比特的计数器初始值设置为一个预设的值(IV),并按照预先确定的规则($\mod 2^n$)增加。为了更好的随机性,增加的值可以根据增加的分组数来确定。下图所示的就是计数器模式:
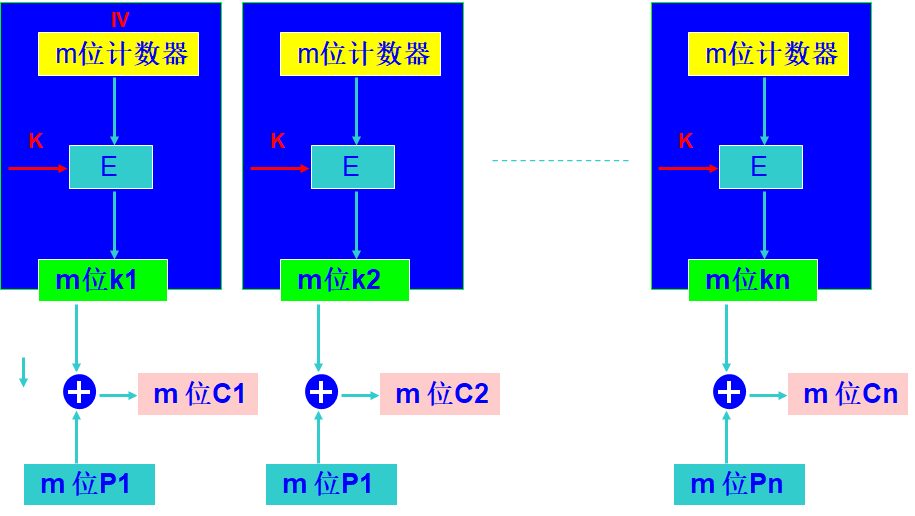
安全性:
- 本质上是同步流密钥,密钥流独立于明文和密文,但由于计数器的递增机制,密钥与计数器所记的数字有关。
- 不保留分组层。
- 传输错误的影响:$C_i$ 有一位传错,只会对明文 $P_i$ 的同一位置产生影响。这就避免了错误的传播。
参考文献
- 《Cryptography and Network Security》 BehrouzA.Forouzan 著
- 《密码学简明教程》 邓元庆 龚晶 石会 编著
- 北航软件学院 《密码学与信息安全基础》课件