本文系MIT深度学习综述手册《Understanding Deep Learning》学习笔记
简介
扩散模型(diffusion model)是一种由编码器和解码器组成的模型。编码器获取数据样本 $\mathbf{x}$ 并将其映射到一系列中间隐变量 $\mathbf{z_1,…,z_T}$ 。解码器反转这个过程,从 $\mathbf{z_T}$ 开始并通过 $\mathbf{z_{T-1},…,z_1}$ 映射回来,直到它最终重新生成一个 $\mathbf{x}$ 。在编码器和解码器中,映射都是随机的而不是确定性的。
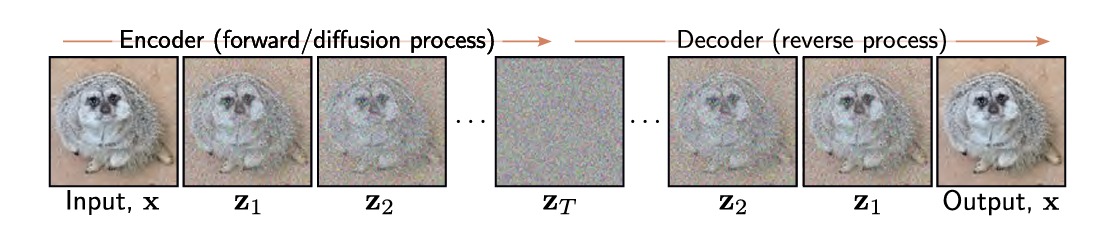
如上图,编码器是预先确定的,它逐渐将输入和白噪声样本混合,通过足够多的步数,最终隐变量的条件分布 $\mathbf{q(z_T \vert x)}$ 和 边缘分布 $\mathbf{q(z_T)}$ 都成为标准正态分布。编码器的随机性是指它不是直接输出一个确定的随机变量 $\mathbf{z_T}$,而是输出一个概率分布 $\mathbf{q(z_T\vert x)}$ 的参数,比如均值和方差。然后,我们可以从这个分布中采样一个随机变量xT,并用解码器重建数据。
编码器的过程是预先指定的,它的作用是将输入数据逐渐加入白噪声,直到变成一个简单的概率分布(比如标准正态分布)。这个过程不需要学习任何参数,只需要确定每一步加入多少噪声,所有学习的参数都在解码器中。在解码器中,训练了一系列网络以在每个相邻的隐变量 $\mathbf{z_t}$ 和 $\mathbf{z_{t-1}}$ 之间向后映射。损失函数鼓励每个网络反转对应的解码器步骤,使得噪声逐渐从表示中去除,直到保留看起来逼真的数据示例。如果想要生成一个新的数据样本,我们可以直接从 $\mathbf{q(z_T)}$ 中采样然后将其送入解码器。
编码器
所谓的扩散过程(或者说前向过程),是指将一个数据样本 $\mathbf{x}$ 映射到一系列与 $\mathbf{x}$ 具有相同大小的中间变量 $\mathbf{z_1,…,z_T}$ 的过程:
\[\begin{array}{l} \mathbf{z_1} & = & \sqrt{1-\beta_1} \mathbf{x} + \sqrt{\beta_1} \epsilon_1 \\ \mathbf{z_t} & = & \sqrt{1-\beta_t} \mathbf{z_{t-1}} + \sqrt{\beta_t} \epsilon_t & \forall t \in 2,...,T \end{array}\]其中 $\epsilon_t$ 是从标准正态分布中提取的噪声,式子中的第一项是为到目前为止添加的所有噪声加上一个衰减系数,第二项是加上更多噪声。超参数 ${ \beta_t } \in [0,1]$ 决定噪声混合的速度,统称为噪声计划(noise schedule)。这可以等价地写成:
\[\begin{array}{l} q(\mathbf{z_1 | x}) & = & Norm_{\mathbf{z_1}} \left[ \sqrt{1-\beta_1} \mathbf{x}, \beta_1 \mathbf{I} \right] \\ q(\mathbf{z_t | z_{t-1}}) & = & Norm_{\mathbf{z_t}} \left[ \sqrt{1-\beta_t} \mathbf{z_{t-1}}, \beta_t \mathbf{I} \right] & \forall t \in 2,...,T \\ \end{array}\]其中 $Norm$ 的第一项表示正态分布的均值,第二项表示方差。通过足够的步数 $T$ ,原始数据的所有痕迹都被去除,并且 $q(\mathbf{z_T \vert x}) = q(\mathbf{z_T})$ 成为标准正态分布。我们可以给出给定原始数据 $\mathbf{x}$ 后,所有隐变量的联合分布。这个分布可以用一个马尔可夫链来定义,也就是说,每个隐变量只依赖于前一个隐变量:
\[q(\mathbf{z_{1...T}|x}) = q(\mathbf{z_1 | x}) \prod_{t=2}^{T} q(\mathbf{z_t | z_{t-1}})\]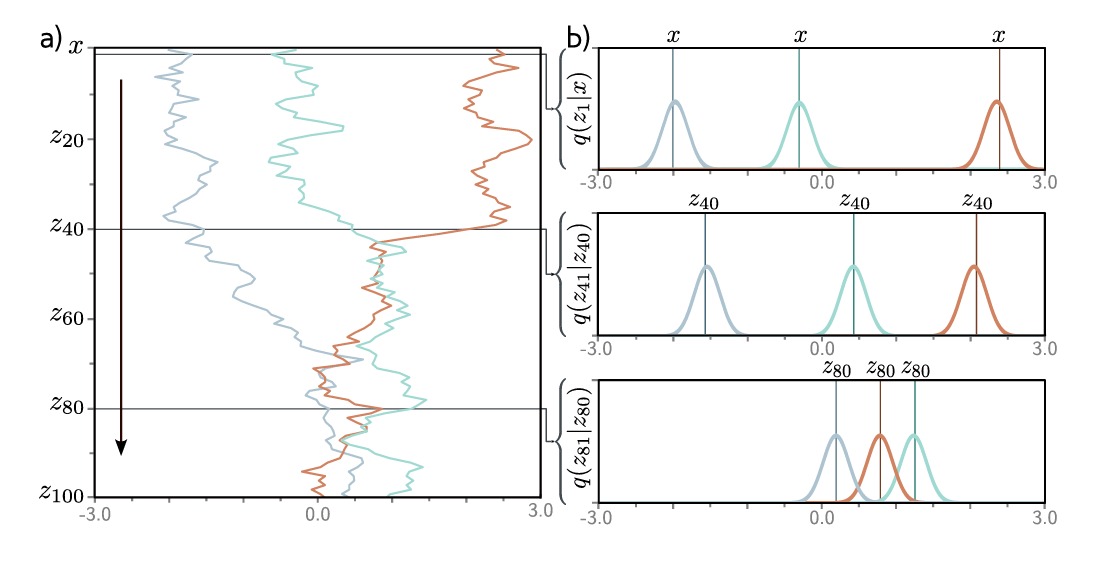
如上图,我们以一个一维数据样本 $x$ 为例,可以看到当我们以不同的 $x$ 作为输入时,经过扩散过程,这三个示例趋向于向0移动,并且分布也逐渐趋近于标准正态分布。
扩散核
为了训练解码器来反转上述过程,我们将为同一个样本 $\mathbf{x}$ 生成多个样本 $\mathbf{z_t}$ ,但是当 $t$ 很大时,使用前面的方法依次生成这些样本是很耗时的。幸运的是,$q(\mathbf{z_t \vert x})$ 有一个封闭形式的表达式,它允许我们在给定初始数据 $\mathbf{x}$ 后直接生成 $\mathbf{z_t}$ 而无需计算中间变量。这被称为扩散核(diffusion kernel)。
为了导出 $q(\mathbf{z_t \vert x})$ 的表达式,我们来考虑前向过程的前两步:
\[\begin{array}{l} \mathbf{z_1} & = & \sqrt{1-\beta_1} \mathbf{x} + \sqrt{\beta_1} \epsilon_1 \\ \mathbf{z_2} & = & \sqrt{1-\beta_2} \mathbf{z_1} + \sqrt{\beta_2} \epsilon_2 \end{array}\]将第一个表达式代入第二个表达式,可以得到:
\[\begin{array}{l} \mathbf{z_2} & = & \sqrt{1-\beta_2} \left( \sqrt{1-\beta_1}\mathbf{x} + \sqrt{\beta_1}\epsilon_1 \right) + \sqrt{\beta_2} \epsilon_2 \\ & = & \sqrt{1-\beta_2} \left( \sqrt{1-\beta_1}\mathbf{x} + \sqrt{1-(1-\beta_1)}\epsilon_1 \right) + \sqrt{\beta_2} \epsilon_2 \\ & = & \sqrt{(1-\beta_2)(1-\beta_1)}\mathbf{x} + \sqrt{(1-\beta_2)-(1-\beta_2)(1-\beta_1)}\epsilon_1 + \sqrt{\beta_2} \epsilon_2 \\ \end{array}\]最后两项是均值正态分布的独立样本,方差分别为 $1-\beta_2 - (1-\beta_2)(1-\beta_1)$ 和 $\beta_2$ 。将二者看成一个整体,其均值仍然为 0 ,方差为二者方差之和,即 $1-(1-\beta_2)(1-\beta_1)$ ,因此我们有如下表示:
\[\mathbf{z_2} = \sqrt{(1-\beta_2)(1-\beta_1)} \cdot \mathbf{x} + \sqrt{1-(1-\beta_2)(1-\beta_1)} \cdot \epsilon\]其中 $\epsilon$ 也是来自标准正态分布的样本。如果我们延续这个过程,可以得到:
\[\mathbf{z_t} = \sqrt{\alpha_t} \cdot \mathbf{x} + \sqrt{1-\alpha_t} \cdot \epsilon\]其中 $\alpha_t = \prod_{s=1}^{t} 1-\beta_s$ ,我们可以用概率形式将其等价地表达为:
\[q(\mathbf{z_t \vert x}) = Norm_{\mathbf{z_t}} \left[ \sqrt{\alpha_t}\cdot \mathbf{x}, (1-\alpha_t)\mathbf{I} \right]\]对于任何起始数据点 $\mathbf{x}$ ,变量 $\mathbf{z}$ 服从已知均值和方差的正态分布。因此如果我们不关心中间变量的演化历史,则很容易从 $q(\mathbf{z_t \vert x})$ 生成样本。
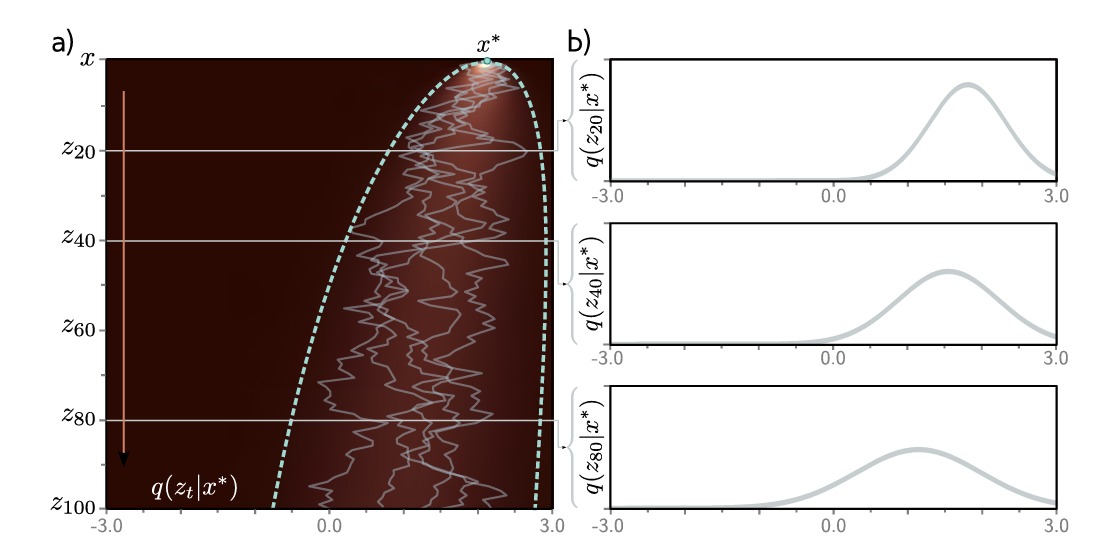
如图,点 $x^{\ast} = 2.0$ 通过隐变量传播(左图中的五个路径),可以看到扩散核的均值向 0 移动并且其方差随着 $t$ 的增加而增加。右图中的概率分布也证实了这一点。这意味着无需计算中间变量即可直接采样。
边缘分布
下面我们引入边缘分布(marginal distribution)的概念,边缘分布 $q(\mathbf{z_t})$ 是当给定了初始点 $\mathbf{x}$ 的概率分布,和给定了每个初始点的可能的扩散路径之后,我们所观察到的 $\mathbf{z_t}$ 的分布。
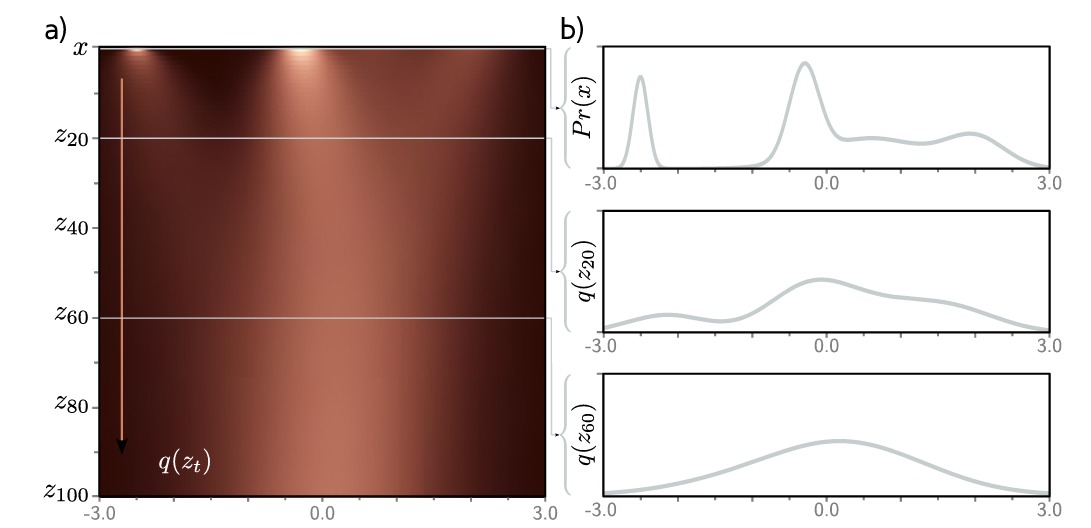
如上图,给定均值为0方差为1的初始密度 $Pr(x)$ ,扩散过程通过隐变量 $z_t$ 并将其移向标准正态分布时逐渐模糊分布,热图的每一条水平线代表了对应的边际分布。我们可以通过在联合分布 $q(\mathbf{x,z_1,…,z_t})$ 中边缘化除了 $\mathbf{z_t}$ 之外的所有变量来计算:
\[\begin{array}{l} q(\mathbf{z_t}) & = & \int \int q(\mathbf{z_t,...,z_1,x}) d\mathbf{z_{t-1,...,1}}d\mathbf{x} \\ & = & \int \int q(\mathbf{z_t,...,z_1 \vert x})Pr(\mathbf{x}) d\mathbf{z_{t-1,...,1}}d\mathbf{x} \end{array}\]然而由于我们现在引入了扩散核,因此我们可以跳过中间变量,等价的写成:
\[q(\mathbf{z_t}) = \int q(\mathbf{z_t \vert x})Pr(\mathbf{x}) d\mathbf{x}\]因此如果我们从数据分布 $Pr(\mathbf{x})$ 中重复采样,并将扩散核叠加到每个样本上,结果就是边缘分布。但是边缘分布不能写成封闭的形式,即不能用数学表达式表出,因为我们不知道原始数据分布 $P(\mathbf{x})$。
条件分布 $q(\mathbf{z_{t-1} \vert z_t})$
在前面我们定义了条件概率 $q(\mathbf{z_t \vert z_{t-1}})$ ,根据贝叶斯定理,我们可以得到它的扭转形式:
\[q(\mathbf{z_{t-1} \vert z_t}) = \frac{q(\mathbf{z_t \vert z_{t-1}})q(\mathbf{z_{t-1}})}{q(\mathbf{z_t})}\]但是这不能实际地用于计算,因为我们无法计算 $q(\mathbf{z_{t-1}})$ ,这也符合我们的直觉,我们在每个阶段都将原始数据的样本和噪声混合在一起,除非我们得到起点,否则无法一步步推出来。
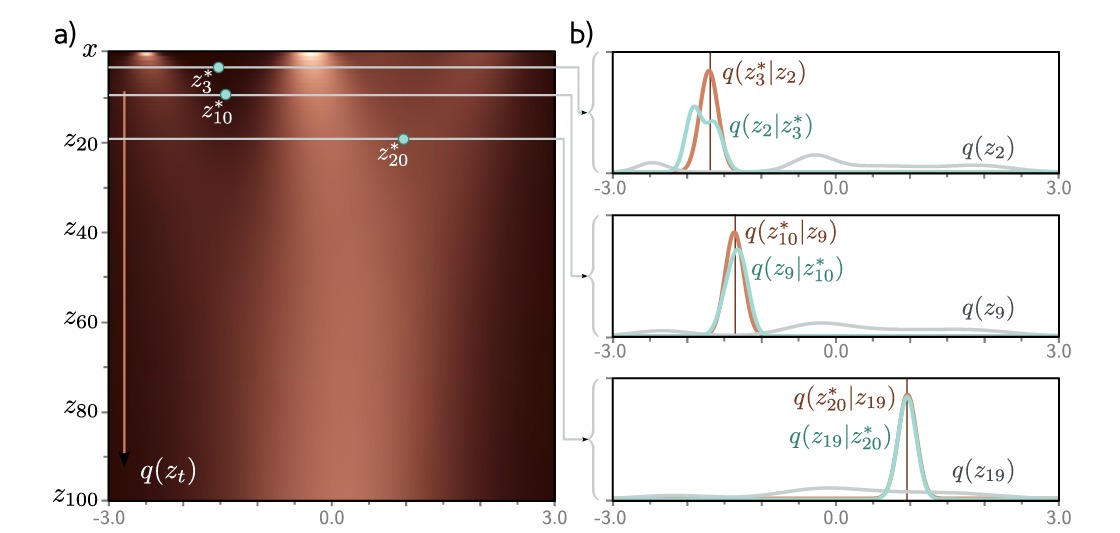
如图,对于这个简单的一维数据分布的例子,我们可以看到总的来说它们不是正态分布的,但是可以用正态近似。
条件扩散分布 $q(\mathbf{z_{t-1} \vert z_t ,x})$
有一个与编码器相关的最终分布需要考虑,我们在上面注意到,我们无法找到条件分布 $q(\mathbf{z_{t-1} \vert z_t})$ 因为我们不知道边际分布 $q(\mathbf{z_{t-1}})$,然而由于我们知道起始变量 $\mathbf{x}$ ,而且我们知道之前的分布 $q(\mathbf{z_{t-1} \vert x})$ ,这样我们就可以得到可以计算的 $q(\mathbf{z_{t-1} \vert z_t ,x})$ 。
计算这个分布的目的是为了训练解码器,在解码过程中我们已知隐向量 $\mathbf{z_t}$ 和原始输入样本 $\mathbf{x}$ ,我们仍然可以遵照贝叶斯公式来计算 $q(\mathbf{z_{t-1} \vert z_t ,x})$ :
\[\begin{array}{l} q(\mathbf{z_{t-1} \vert z_t,x}) & = & \frac{q(\mathbf{z_t \vert z_{t-1}, x}) q(\mathbf{z_{t-1} \vert x})}{q(\mathbf{z_t \vert x})} \\ & \varpropto & q(\mathbf{z_t \vert z_{t-1}}) q(\mathbf{z_{t-1} \vert x}) \\ & = & Norm_{\mathbf{z_t}} \left[ \sqrt{1-\beta_t} \cdot \mathbf{z_{t-1}},\beta_t \mathbf{I} \right] Norm_{\mathbf{z_{t-1}}} \left[ \sqrt{\alpha_{t-1}} \cdot \mathbf{x},(1-\alpha_t) \mathbf{I} \right] \\ & = & Norm_{\mathbf{z_{t-1}}} \left[ \frac{1}{\sqrt{1-\beta_t}} \mathbf{z_{t}},\frac{\beta_t}{1-\beta_t} \mathbf{I} \right] Norm_{\mathbf{z_{t-1}}} \left[ \sqrt{\alpha_{t-1}} \cdot \mathbf{x},(1-\alpha_t) \mathbf{I} \right] \\ \end{array}\]在前两行之间,我们使用了 $q(\mathbf{z_t \vert z_{t-1},x}) = q(\mathbf{z_{t} \vert z_{t-1}})$ 因为这个扩散过程是马尔可夫的,所有关于 $\mathbf{z_t}$ 的信息都包含在了 $\mathbf{z_{t-1}}$ 中。在第三行和第四行中我们应用了高斯恒等式:
\(Norm_{\mathbf{v}} \left[\mathbf{Aw,B} \right] \varpropto Norm_{\mathbf{w}} \left[ \mathbf{(A^T B^{-1}A)^{-1}A^T B^{-1}v,(A^T B^{-1}A)^{-1}} \right]\) 为了进一步改写前述分布,接下来我们用第二高斯恒等式:
\[Norm_{\mathbf{w}} [\mathbf{a,A}] \cdot Norm_{\mathbf{w}} [\mathbf{b,B}] \\ \varpropto Norm_{\mathbf{w}} \left[ \mathbf{(A^{-1} + B^{-1})^{-1} (A^{-1}a + B^{-1}b), (A^{-1} + B^{-1})^{-1}} \right]\]这样我们可以将前面的 $\mathbf{z_{t-1}}$ 的分布合并为:
\[q(\mathbf{z_{t-1} \vert z_t , x}) = Norm_{\mathbf{z_{t-1}}} \left[ \frac{1-\alpha_{t-1}}{1-\alpha_t} \sqrt{1-\beta_t} \mathbf{z_t} + \frac{\sqrt{\alpha_{t-1}}\beta_t}{1-\alpha_t} \mathbf{x}, \frac{\beta_t (1-\alpha_{t-1})}{1-\alpha_t}\mathbf{I} \right]\]请注意,以上方程中的比例常数必须抵消,因为最终结果已经是正确归一化的概率分布。
参考文献
- 《Understanding Deep Learning》Simon J.D. Prince
- The Annotated Diffusion Model https://huggingface.co/blog/annotated-diffusion