本文系MIT深度学习综述手册《Understanding Deep Learning》学习笔记
图简介
图是一种非常通用的结构,由一组节点组成,其中节点通过边来连接。现实世界中的一些对象可以自然地采用图的形式,例如道路网络可以被视为图,其中节点是物理位置,边代表它们之间的道路;化学分子是一种小的图,其中节点代表原子,边代表化学键。此外,许多数据集也可以用图来表示,例如,社交网络是一种图,其中节点是人,边缘代表它们之间的社交关系;科学文献可以看作一个图,其中节点是论文,边表示涉及这些变量的计算。
此外,集合可以被视为一个图,其中每个成员都是一个节点,并相互连接。图像可以被视为具有规则拓扑的图,其中每个像素都是一个节点,其边缘指向八个相邻像素。
图的类型
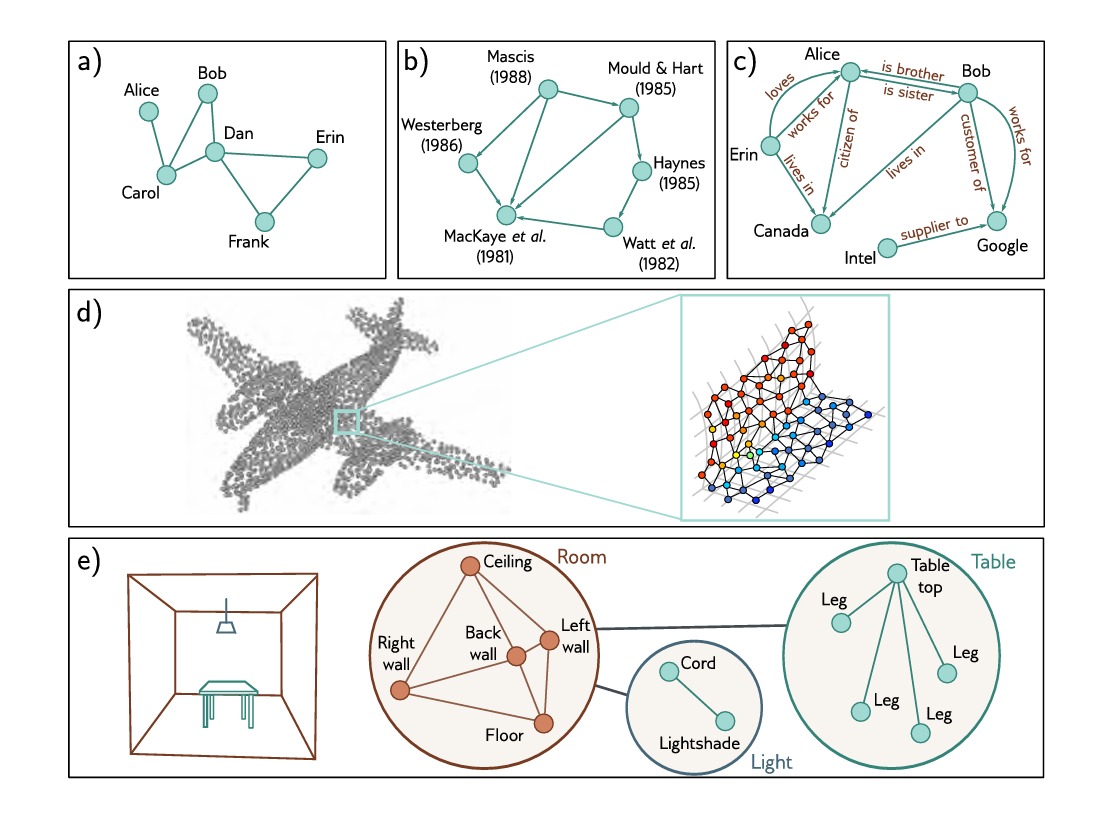
图可以通过多种方式进行分类。a)中的社交关系中包含的是无向边,这种关系没有方向性;而b)中的引文网络包含有向边,论文之间的引用关系本质上是单向的。c)描述了一个知识图,它通过定义对象之间的关系来编码关于对象的一组事实,这是一个有向异构多重图。它是异构的,因为节点可以代表不同类型的实体(如人、国家、公司),它又是一个多重图,因为任何两个节点之间都可以有不同类型的多条边。通过将每个点连接到其最近的邻居,可以将d)中的表示飞机的点云转换为图。e)代表了一个层次图,桌子、灯和房间分别由表示其各自组件的相邻性的图形来描述,这三个图本身又是另一个图中的节点,该图表示更大的对象的拓扑。
所有类型的图都可以使用深度学习进行处理,我们重点探讨的是无向图。
图的表示
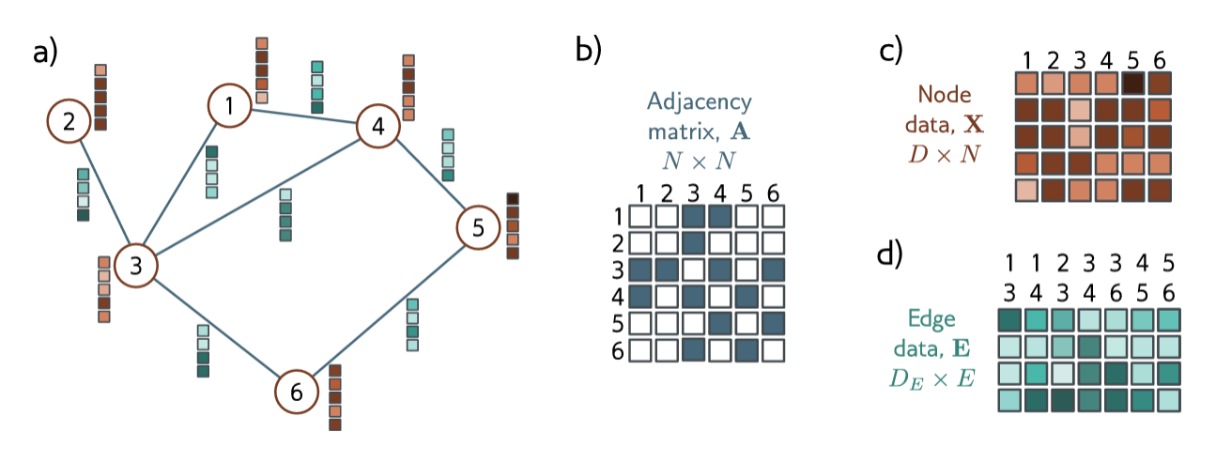
一个图由 $N$ 个节点和 $E$ 条边组成,它可以由三个矩阵 $\mathbf{A,X,E}$ 表示。其中 $\mathbf{A}$ 表示节点之间的邻接矩阵($N \times N$),即如果点 $m$ 和点 $n$ 之间有一条边邻接,那么 $\mathbf{A}[m,n] = 1$。$\mathbf{X}$ 表示节点的 $embedding$,大小为 $D \times N$,其中的第 $n$ 个列向量 $\mathbf{x^{(n)}}$ 即表示第 $n$ 个节点的长度为 $D$ 的 $embedding$ 。类似的,$\mathbf{E}$ 表示边的 $embedding$,大小为 $D_e \times N$,其中的第 $e$ 个列向量 $\mathbf{e^{(n)}}$ 即表示第 $e$ 条边的长度为 $D_e$ 的 $embedding$ 。
为了简单起见,我们后面首先考虑只有节点 $embedding$ 的图。
节点索引置换
图的节点其实并没有一个严格的顺序,这意味着我们可以用不同的方式为图节点选择索引,而索引不同的情况下,图的表示矩阵也就会发生变化。换言之,我们通过选择不同索引的方式,即使改变了图的表示矩阵,却没有改变图表示的含义,这一点和处理图像时的像素点矩阵大不相同。
我们可以通过引入置换矩阵 $\mathbf{P}$ 来表示这一性质。置换矩阵的每一列(或每一行)都有且仅有一个位置是1而其余位置都是0,当 $\mathbf{P}[m,n]=1$ 时,这表示前一个图的第 $m$ 个节点通过变换之后将成为新图中的第 $n$ 个节点。以下公式揭露了使用置换矩阵生成新图的关系:
\[\mathbf{X'=XP} \\ \mathbf{A'=P^T A P}\]其中 $\mathbf{A’}$ 的置换可以这样理解,我们使用一个独热行向量 $\mathbf{v_n}$,它表示第 $n$ 个节点,它的第 $n$ 个位置为1而其余位置为0。我们可知 $\mathbf{v_n’A’}$ 即表示了节点 $n$ 在新图中的邻接情况。而从另一个方面来说,我们可以通过 $\mathbf{ v_n’P^T=v_n}$ 得到原图的独热向量,并通过右乘 $\mathbf{A}$ 得到原图中的临界情况,再推广到新图。其实由于置换矩阵具备性质 $\mathbf{P^T = P^{-1}}$ ,因此这一过程可以通过过渡矩阵和相似矩阵的关系来理解。
图神经网络问题分类
图神经网络将节点 $embedding$ 矩阵 $\mathbf{X}$ 和邻接矩阵 $\mathbf{A}$ 作为输入,并使其通过 $K$ 层,在每一层都将更新节点 $embedding$ 以创建中间的隐藏表示 $\mathbf{H}_k$,并最终计算输出的 $\mathbf{H}_K$。在网络起始部分,输入节点 $embedding$ 只包含关于节点自身的信息,最后模型输出的 $\mathbf{H}_K$ 的每一列都包括关于图中节点及其上下文的信息。这类似于 transformer 中的单词 $embedding$,在开始只表示单词,但在最后表示句子上下文中的单词含义。
我们首先描述图神经网络处理的问题类型以及每种问题相关的损失函数。
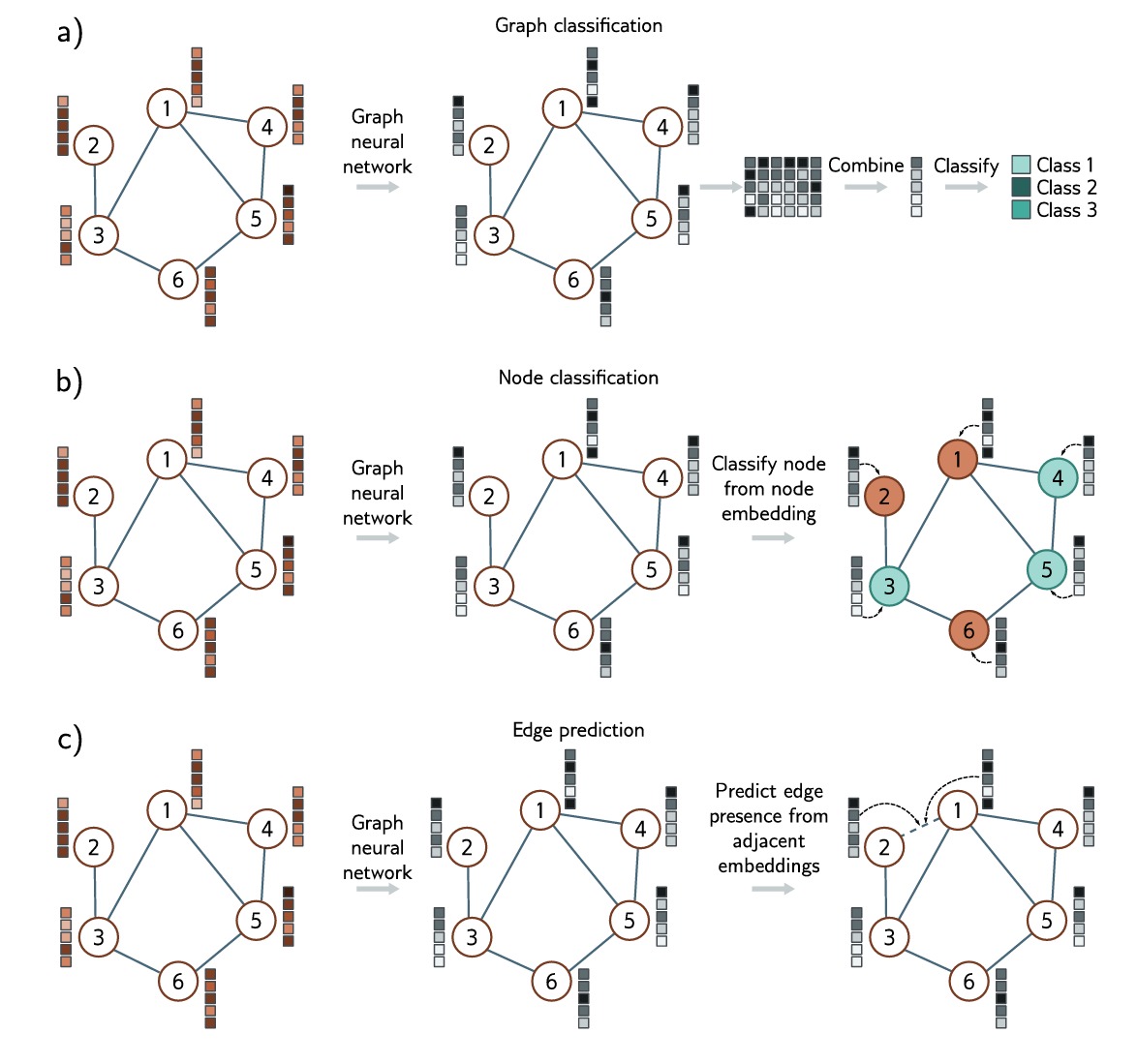
图级任务
网络利用整体结构和节点 $embedding$,从整个图中赋予一个标签或者估计一系列值。例如预测分子变成液体的温度(回归任务),或者分子是否对人类有毒(分类任务)。
对于图级任务,将输出节点 $embedding$ 进行组合,并通过线性变换或神经网络将结果向量映射到固定大小的向量。对于回归,使用最小二乘损失来计算结果和ground truth之间的匹配情况;对于分类任务,输出将通过一个sigmoid函数,然后计算二进制交叉熵损失,这里输出 $y$ 可以按如下计算:
\[y=sig \left[ \beta_K + \mathbf{\omega}_K \mathbf{H}_K \mathbf{1} /N \right]\]其中标量 $\beta_K$ 和大小为 $1\times D$ 的 $\omega_K$ 其参数通过学习得到。$\mathbf{1}$ 是一个全1矩阵,用于将 $\mathbf{H}_K$ 的每一行相加到一起,然后再除以 $N$ 以起到平均池化的作用。
点级任务
网络仍然利用整体结构和节点 $embedding$ ,为每个节点赋予一个标签或估计一系列值。例如给一个前节中邻接点云结构的图,为每个节点判断它是不是位于机翼上。
损失函数和图级任务的类似,唯一的区别是我们单独为每个节点计算输出:
\[y^{(n)}=sig \left[ \beta_K + \mathbf{\omega}_K \mathbf{h}_K^{(n)} \right]\]边级任务
网络预测节点 $n$ 和 $m$ 之间是否应该有边缘,例如,在社交网络中,网络可能会预测两个人是否有共同的爱好,并建议他们联系。这是一个二进制分类任务,其中两个节点 $embedding$ 必须映射到边缘存在概率的单个数字。一种可能性是采用节点 $embedding$ 的点积,并将结果通过 sigmoid 函数来得到概率:
\[y^{(mn)} = sig \left[ \mathbf{h}^{(m)T} \mathbf{h}^{(n)} \right]\]归纳式和直推式
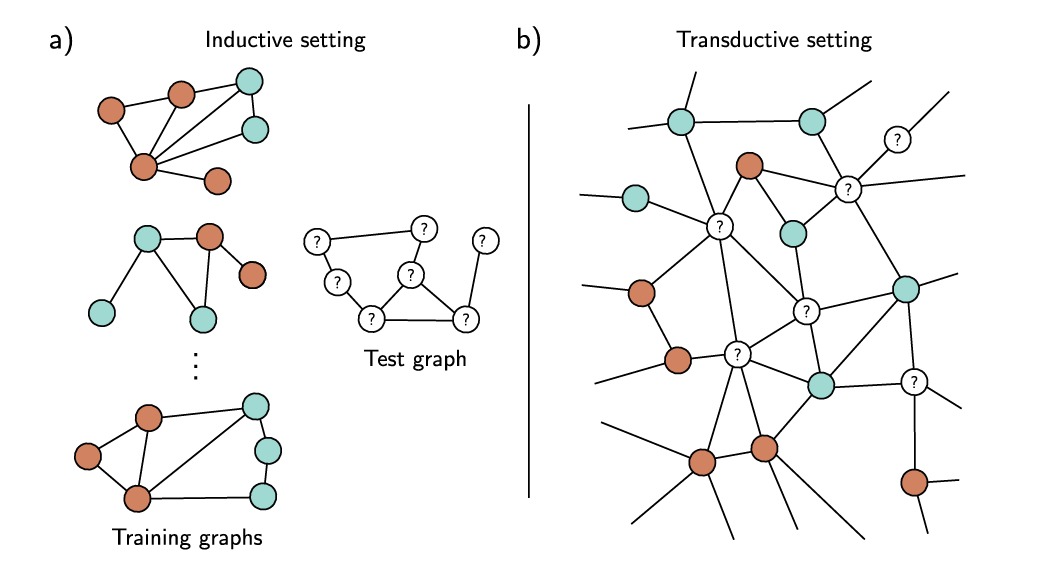
如图a),我们一般比较习惯的网络都是归纳式(inductive)的:我们在一个已经标注完善的数据集上进行训练,使得模型学习从输入到输出的模式,然后我们给出新的测试数据,然后查看模型在新的数据上的训练结果。对于这一过程的理解较为容易,我们可以看作是网络学习了从输入到输出之间的规律。
与之对应的是直推式(transductive)的网络:一个直推式的模型将同时考虑网络中已标注和未标注的数据,它的目的是处理网络中未标注的部分,这有时也被称作半监督学习(semi-supervised learning)。其优点是可以利用网络中的未知部分,但缺点是不能像归纳式模型一样进行推广。
这两种问题在图领域都很常见。有时我们有很多带标签的图,并学习图和标签之间的映射。例如我们可能有许多分子,每个分子标记有毒/无毒,我们学习这种映射规则,并将其应用到一个新分子。然而,有时是一个单一的图。在科学论文引用的图表中,我们可能有指示某些节点的领域(如生物学)的标签,我们希望标记其余节点(如物理学等领域),在这里,二者是必然连接在一起的。
图级任务只发生在有训练和测试的归纳式模型中,然而点级任务和边级任务可以发生在任何一种设置中。在直推式情况下,损失函数最大限度地减少模型输出和已知情况的ground truth的失配,新的预测是通过进行前向传播并检索ground truth未知的情况来计算的。
图卷积网络
有很多类型的图神经网络,这里我们首先关注基于空间的卷积图神经网络,即GCN(Graph Convolutional Network),这些模型是卷积的,因为它们通过聚集来自附近节点的信息来更新每个节点,因此它们会引发一种关系归纳偏置(relational inductive bias),即优先考虑来自于邻居的信息。
GCN的每一层可以看作一个函数 $\mathbf{F[\bullet]}$ ,其参数表示为 $\mathbf{\Phi}$。该函数将节点 $embedding$ 和邻接矩阵作为输入,并输出更新过后的节点 $embedding$,这一网络可以表达如下:
\[\mathbf{H}_1 = \mathbf{F[X,A,\phi_0]} \\ \mathbf{H}_2 = \mathbf{F[H_1,A,\phi_1]} \\ ... \\ \mathbf{H}_K = \mathbf{F[H_{K-1},A,\phi_{K-1}]}\]其中 $\mathbf{X}$ 为输入,$\mathbf{A}$ 为邻接矩阵,$\mathbf{H}_k$ 表示更新过的第 $k$ 层的节点 $embedding$,$\phi_k$ 表示该层的参数。
等变性和不变性
我们之前已经注意到,图中节点的索引可以有不同的顺序,这些索引的不同排列并不会改变图,因此任何模型都必须尊重这一特性。因此对于节点索引的排列,每个层都必须是等变的(equivariance)。用数学术语来说,如果 $\mathbf{P}$ 是一个置换矩阵,那么我们必须有:
\[\mathbf{H}_{k+1} \mathbf{P} = \mathbf{F}[\mathbf{H}_k \mathbf{P},\mathbf{P^T AP},\phi_k]\]对于节点分类任务和边缘预测任务,其输出对应节点序列的顺序应当也是等变的。对于图级任务来说,最后一层聚合了整个图的信息,因此其输出对节点顺序是具备等变性的。这可以从最后一步输出的公式中显然看到:
\[y=sig \left[ \beta_K + \omega_K \mathbf{H}_K \mathbf{1}/N \right] = sig \left[ \beta_K + \omega_K \mathbf{H}_K \mathbf{P1}/N \right]\]在对于图像的卷积神经网络中,卷积层和池化层在平移操作上是可以保持等变,但是对于其他更一般的变换则不能保证。然而,对于图来说,这一性质是无论如何排列均可以保持的。
参数共享
在应用于图像时,我们认为将全连接的网络并不是明智的,应为这需要网络学习如何在每个图象位置分别识别物体。相反地,我们使用卷积层,对图像中每个位置进行相同的处理,这减少了参数的数量,并引入了归纳偏置。迫使模型以相同的方式处理图像的每个部分。
对于图中的节点也可以进行相同的论证,我们可以学习一个与每个节点相关联的参数的模型,然而这就必须独立地学习每个位置的连接的含义。如果我们在每个节点使用相同的参数,那么就可以减少参数的数量,并且在整个图中共享网络在每个节点学到的东西。
回顾卷积神经网络,卷积核通过从其邻居获取信息的加权和来更新变量。我们可以理解为每个邻居向这一变量发送一条消息,该变量聚合这些信息然后更新。当我们考虑图象时,邻居就是在当前位置周围固定大小的正方形区域的像素,因此每个位置的空间关系是相同的。但是当考虑一个图时,每个节点可能具有不同数量的邻居,而且我们也不能和像素点一样分辨不同节点的上下左右位置。
GCN层示例
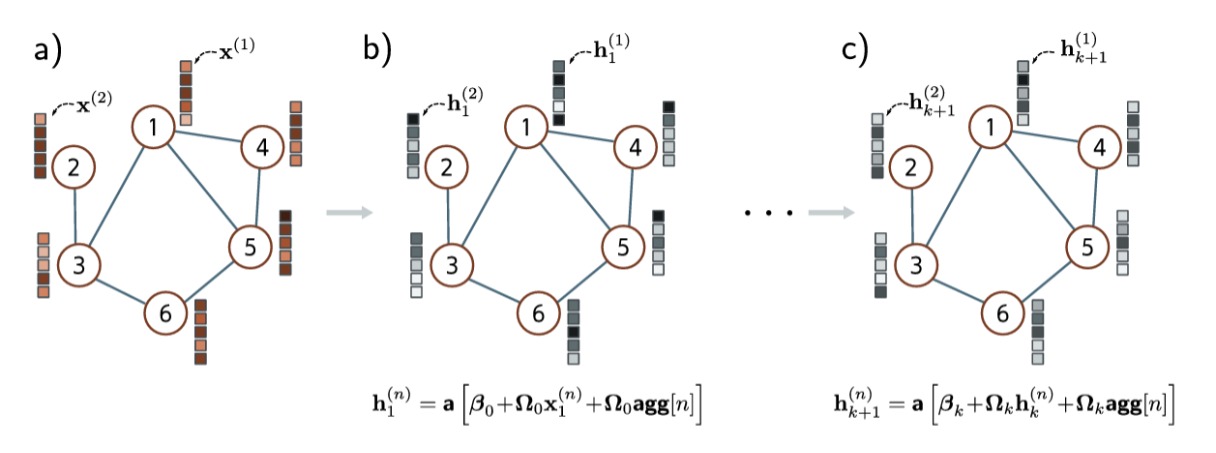
我们给出一个简单的GCN层示例,在第 $k$ 层的每个节点 $n$ 上,我们把来自节点邻居的 $embedding$ 相加来聚合信息:
\[\mathbf{agg}[n,k] = \sum_{m \in ne[n]} \mathbf{h}_k^{(m)}\]之后我们引入一个线性变换 $\mathbf{\Omega}_k$ 作用在聚合结果和 $\mathbf{h}_k^{(n)}$ 上,然后加上一个偏置项 $\beta_k$,将结果通过一个激活函数 $\mathbf{a}[\bullet]$,该函数对向量中的每个元素单独作用。其公式表示如下:
\[\mathbf{h}_{k+1}^{(n)} = \mathbf{a} \left[ \mathbf{\beta}_k + \mathbf{\Omega_k \cdot h_k^{(n)}} + \mathbf{\Omega_k}\cdot \mathbf{agg}[n,k] \right]\]我们可以进一步地通过引入矩阵变换简化这一表示。邻接矩阵的每一列即表示了该点与其他点的邻接情况,$\mathbf{H}_k$ 右乘邻接矩阵即表示对 $\mathbf{H}_k$ 中的列向量进行线性组合,具体来说运算后的结果中,每一列将更新所有邻接点的和。矩阵表示如下:
\[\begin{matrix} \mathbf{H_{k+1}} & = & \mathbf{a\left[\beta_k 1^T + \Omega_k H_k + \Omega_k H_k A \right]} \\ & = & \mathbf{a\left[\beta_k 1^T + \Omega_k H_k(I+A) \right]} \end{matrix}\]该层设计满足:它对节点索引的排列是等变的,可以处理任意数量的邻接点,并且利用图结构提供归纳偏置,在整个图中共享参数。
任务举例
示例任务:图分类
我们现在描述一个图神经网络,该网络将一个分子分类为有毒或无毒。网络输入是邻接矩阵 $\mathbf{A}$ 和节点 $embedding$ 矩阵 $\mathbf{X}$。邻接矩阵 $\mathbf{A} \in \mathbb{R}^{N\times N}$ 来源于分子结构,节点 $embedding$ 矩阵 $\mathbf{X} \in \mathbb{R}^{118\times N}$ 的每一列是一个独热向量,它表示位于该位置的原子是元素周期表中118个元素中的哪一个。节点 $embedding$ 可以通过第一层的权重矩阵 $\mathbf{\Omega}_0 \in \mathbb{R}^{118\times D}$ 转换为任意大小。
网络结构可以表示为:
\[\begin{matrix} \mathbf{H}_1 & = &\mathbf{a\left[\beta_0 1^T + \Omega_0 X(I+A) \right]} \\ \mathbf{H}_2 & = &\mathbf{a\left[\beta_1 1^T + \Omega_1 H_1(I+A) \right]} \\ & ... \\ \mathbf{H}_K & = & \mathbf{a\left[\beta_{K-1} 1^T + \Omega_{K-1} H_{K-1}(I+A) \right]} \\ f[\mathbf{X,A,\Phi}] & = & sig\left[ \beta_K + \omega_K \mathbf{H_K 1}/N \right] \end{matrix}\]最终的输出即一个概率,表示了该分子是否是有毒的。
给定 $I$ 个训练图 ${ \mathbf{X_i,A_i} }$ 及其标签 $y_i$,参数 $\mathbf{\Phi = { \beta_K, \Omega_K }_{K = 0}^{N}}$ 可以通过随机梯度下降和交叉熵损失来学习。全连接网络,CNN和 transformer 都可以通过并行来批处理,为此,在处理时会将批处理元素连接成一个更高维的向量。然而由于不同的图之间的节点个数是不同的,矩阵 $\mathbf{X}_i$ 和 $\mathbf{A}_i$ 的大小也不相同,我们无法直接将它们连接成三维向量。在这里我们引入一个简单的技巧,让我们可以并行地进行前向和反向传播,批处理中的图被视为单个大型图的不相交分量。平均池化仅在单个图上进行,以使每个图都有一个单一表示,以输入损失函数。
示例任务:点分类
我们考虑一个具有数百万节点的商业大小的图,一些节点有 ground truth 的二进制标签,我们需要标记剩余的节点。网络的主体与上一个例子相同,但是最后一层会不一样,在这里最后一层输出一个大小 $1\times N$ 的向量:
\[\mathbf{f[X,A,\Phi] = sig\left[ \beta_K 1^T + \omega_K H_K \right]}\]其中 sigmoid 函数独立地应用于行向量输入的每个元素。我们仍然使用二进制交叉熵损失,但现在只在我们知道 ground truth 的节点上。
训练这个网络会带来两个问题。首先,图的规模非常大,如果在前向传播中存储每个网络层的节点 $embedding$,这将涉及存储一个数倍于整个图大小的结构。其次,我们只有一个图,所以如何执行随机梯度下降和如何形成batch也都是问题。
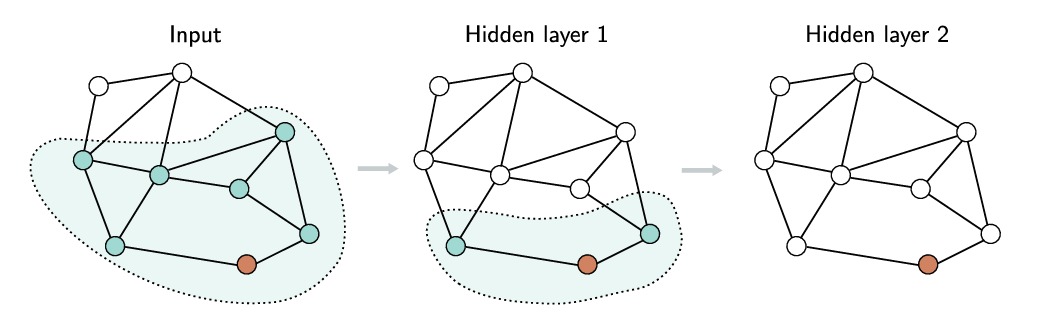
如上图,一种选择batch的方法是在每个训练步骤选择标记节点的随机子集。每个节点都依赖于其再上一层中的邻居,进一步地,这些邻居又取决于它们在更之前的层中的邻居,通过这种方式我们为一个节点选取一个感受野,感受野的大小被称为k跳邻域(k-hop neighborhood)。我们可以使用形成一个batch节点的k跳邻域的并集图执行梯度下降步骤,让其余的输入不起作用。
然而,如果有很多层,并且图是密集连接的,那么每个输入节点都可能在输出的感受野中,这不会减小图的大小。这就是图展开(graph expansion problem)问题。解决这个问题的两种方法是邻域采样(neighborhood sampling)和图分割(graph partitioning)。
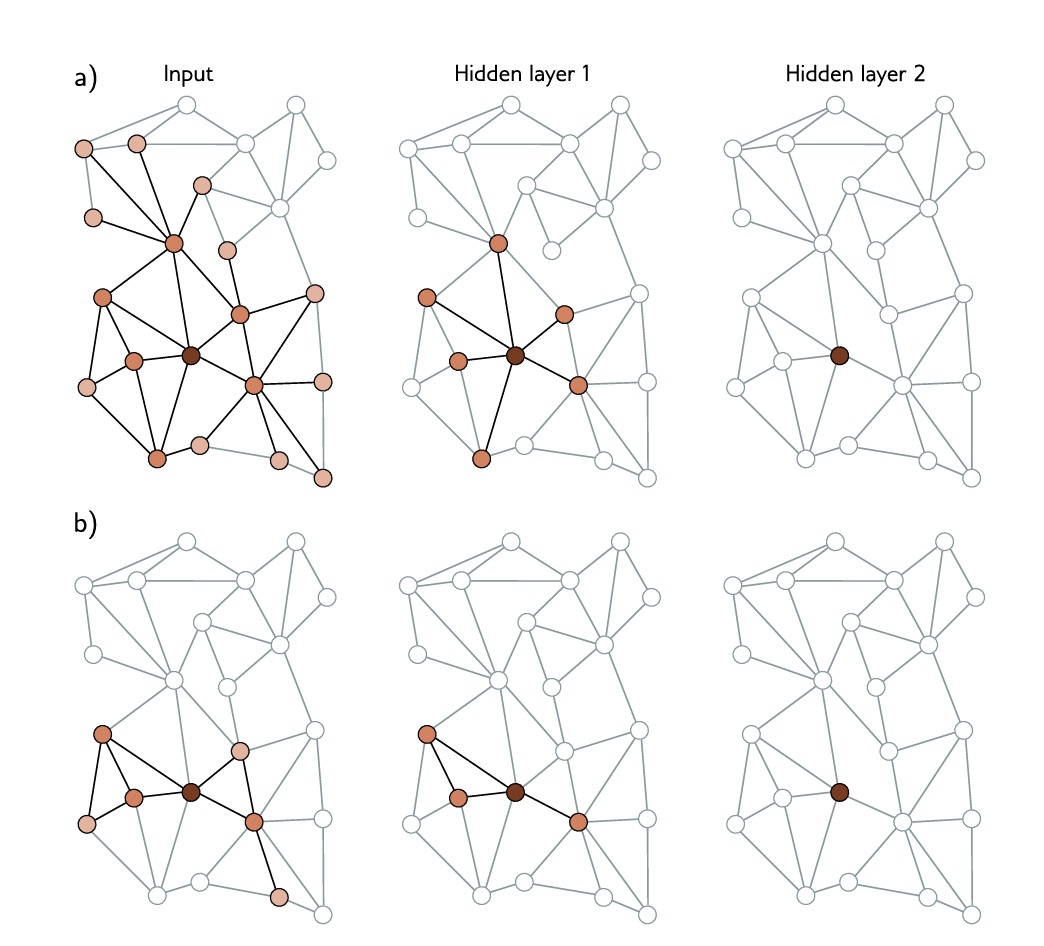
邻域采样:我们从选择的batch节点开始,随机采样前一层中的固定数量的邻居,以此类推,图的大小仍然随着每一层的增加而增加,但是这是一种更加可控的方式。这是对每个batch都会重新进行的,因此即使同一batch,采样两次,参与贡献的邻居也会不同。这和dropout有类似指出,并且这一操作也带有正则化的味道。

图分割:图分割是指在处理之前将原始图通过聚类的方式转换为不相交的节点子集(即彼此不连接的较小的图)。如上图,我们在输入图之后将图划分为更小的子图(划分原则是尽可能去掉的边数量最少)。这些较小的图可以被当做batch。或者可以将它们的随机组合,来形成一个batch(组合时需要从原始图中把去掉的边补上)。
我们选定一种生成batch的方法,然后就可以按照和归纳式模型相同的方式训练网络参数,即根据需要将标记的节点划分为训练集、测试集和验证集。为了进行推理,我们使用未知节点的k跳邻域来计算其预测。
GCN层的变体
我们此前介绍了一种较为简单的GCN层,即通过 $embedding$ 矩阵 $\mathbf{H}$ 和 $\mathbf{A+I}$ 相乘,来从邻接点上提取信息。我们现在重新审视这个问题,可以从两个角度尝试不同的方法:一是当前的 $embedding$ 和其邻居的聚合结果的结合方式,二是聚合本身的过程。
当前节点和邻接点的结合
在之前的GCN层中,我们计算的过程可以按照如下表示:
\[\mathbf{H_{k+1}} = \mathbf{a\left[\beta_k 1^T + \Omega_k H_k (A+I) \right]}\]在另一个变体中,在将当前节点和邻接点聚合结果相加之前,先乘以因子 $(1+\epsilon_k)$ ,其中 $\epsilon_k$ 是学习的标量,每一层都各不相同。这样计算结果可以表示为:
\[\mathbf{H_{k+1}} = \mathbf{a\left[\beta_k 1^T + \Omega_k H_k (A+(1+\epsilon_k)I) \right]}\]这被称为是对角线增强(diagonal enhancement)。也有相关的变体为当前节点进行线性变换 $\mathbf{\Psi}_k$:
\[\begin{matrix} \mathbf{H}_{k+1} & = & \mathbf{a\left[ \beta_k 1^T + \Omega_k H_k A + \Psi_k H_k \right]} \\ & = & \mathbf{a\left[ \beta_k 1^T + \left[ \Omega_k \ \ \Psi_k \right] \left[ \begin{matrix} \mathbf{H_k A} \\ \mathbf{H_k} \end{matrix} \right] \right]} \\ & = & \mathbf{a\left[ \beta_k 1^T + \Omega_k' \left[ \begin{matrix} \mathbf{H_k A} \\ \mathbf{H_k} \end{matrix} \right] \right]} \end{matrix}\]残差连接
对于残差连接(residual connection)的情况,我们将先对来自邻接点的聚合结果使用激活函数,然后再通过相加或者矩阵连接的方式,把邻接点的聚合结果加到当前节点上。
对于矩阵连接方式,其数学表示如下:
\[\mathbf{H}_{k+1} = \left[ \begin{matrix} \mathbf{a[\beta_k 1^T + \Omega_k H_k A]} \\ \mathbf{H}_k \end{matrix} \right]\]均值聚合
此前的方法通过对节点的 $embedding$ 求和来聚合来自邻接点的信息,但有时候取平均值比取总和要好。如果嵌入信息更重要并且结构信息并不是那么关键,那么这可能是更加优越的,因为邻域贡献的大小将不取决于邻域的数量。其公式表示如下所示:
\[\mathbf{agg[n]} = \frac{1}{| ne[n]|}\mathbf{\sum_{m\in ne[n]} h_m}\]通过引入 $N\times N$ 的度矩阵 $\mathbf{D}$,我们可以以矩阵形式非常巧妙地计算上述公式。度矩阵是一个对角矩阵,其中的每个非零元素都包含相关节点的邻居数量,因此逆矩阵 $\mathbf{D}^{-1}$ 中的每个对角元素包含我们计算平均值所需的分母。因此新的GCN层可以写成:
\[\mathbf{H_{k+1}} = \mathbf{a\left[\beta_k 1^T + \Omega_k H_k (A D^{-1} +I) \right]}\]参考文献
- 《Understanding Deep Learning》Simon J.D. Prince