本文系MIT深度学习综述手册《Understanding Deep Learning》学习笔记
背景问题
Transformer最早起源于自然语言处理(NLP)问题,这一问题不同于卷积神经网络所擅长处理的图像问题,一句话的输入长度/大小,以及不同词汇输入顺序等因素都对这句话的理解起到了非常重要的作用。
例如下面这段话:
The restaurant refused to serve me a ham sandwich because it only cooks vegetarian food. In the end, they just gave me two slices of bread. Their ambiance was just as good as the food and service.
我们可以看到以下一些问题:
- 首先,编码后的输入将会很大。这句话中包含了37个单词,如果每个单词用一个长度为1024的隐向量来表示,那么整个输入长度为 37888,如果是更长的一段文本,那么输入长度会达到数十万甚至上百万。
- 并且,不同的输入是不等长的。我们不能限制一段文本有严格固定的字数,因此我们必须处理可变长的输入,而这一点就意味着我们很难直接应用一个全连接的网络。而且这一点也表明,我们可能需要让不同位置之间的这些单词共享参数(就像卷积神经网络在图像的不同位置都是应用同一套卷积核一样)。
- 还有,单词是具有歧义的。仅仅从语法角度来说,it 可以指代 restaurant,也可以指代 sandwich,为了理解文本,单词 it 应当和 restaurant 联系起来,这也就是后面Transformer中引入的注意力机制。
自注意力机制
一个自注意力块(self-attention block)我们记作 $\mathbf{sa[\bullet]}$,它有 $N$ 个输入 $\mathbf{x_n}$,每个输入都是 $D\times 1$ 维的(即列向量),然后返回 $N$ 个相同大小的输出。在NLP的概念中,一个输入 $\mathbf{x_n}$ 代表一个单词或一个词组。
对于一个自注意力块来说,首先对每个输入计算 $values$:
\[\mathbf{v_n=\beta_v + \Omega_v x_n}\]在这里 $\mathbf{\beta_v}$ 和 $\mathbf{\Omega_v}$ 分别代表偏移(bias)和权重(weight),之后第 $n$ 个输出 $\mathbf{sa[x_n]}$ 是一个 $\mathbf{v_n}$ 的加权和:
\[\mathbf{sa[x_n]}=\sum_{m=1}^{N} a[\mathbf{x_m,x_n}]\mathbf{v_m}\]其中的标量权重 $a[\mathbf{x_m,x_n}]$ 是 $\mathbf{x_m}$ 对 $\mathbf{x_n}$ 的注意力(attention),这 $N$ 个权重都是非负的并且其和为1。
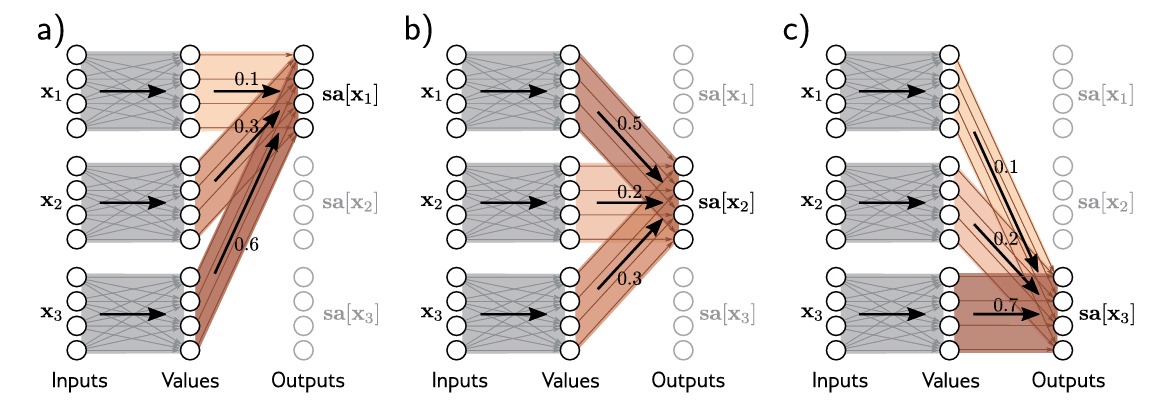
如上图所示,三个输入 $\mathbf{x_1,x_2,x_3}$ 分别计算 $values$,然后各自以不同的权重(红色部分)相加作为输出,分别得到 $\mathbf{sa[x_1],sa[x_2],sa[x_3]}$。
注意力权重计算
在前面的推导中我们知道,对于每个输入 $\mathbf{x_m}$,我们可以独立地得到对应的 $value$:$\mathbf{\beta_v+\Omega_v x_m}$,这一过程是比较熟悉的;对于不同输入,我们可以计算其之间的注意力权重 $a[\mathbf{x_m,x_n}]$,我们下面将重点探讨这部分权重的计算。
我们对输入进行以下两个线性变换:
\[\mathbf{q_n=\beta_q+\Omega_q x_n} \\ \mathbf{k_n=\beta_k+\Omega_k x_n}\]在这里我们将 $\mathbf{q_n}$ 和 $\mathbf{k_n}$ 分别称为 $query$ 和 $key$。之后我们计算二者之间的点积并且通过 softmax 函数进行处理:
\[a[\mathbf{x_m,x_n}]=softmax_m[\mathbf{k^T_{\bullet}q_n}] = \frac{exp[\mathbf{k^T_m q_n}]}{\sum_{i=1}^{N}exp[\mathbf{k^T_i q_n}]}\]$query$ 和 $key$ 是从信息检索领域所继承的说法,我们可以解释为,一个点乘的结果相当于计算了查询内容 $query$ 和关键字 $key$ 之间的相似性。通过这个权值,我们能够分析这个输入对应提取的是什么位置的信息,从而对应地作用到 $value$ 上,生成对应的结果。
矩阵形式
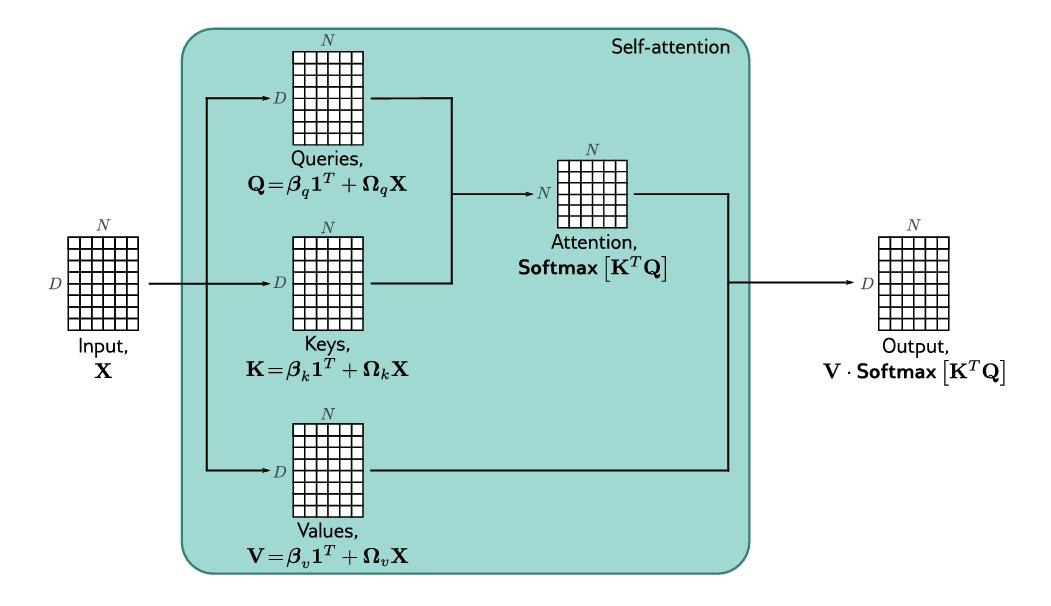
上图表示了矩阵形式下自注意力块的运算过程。如图所示,我们对输入的 $N$ 个向量都分别进行前述运算,最终运算的过程相当于对于大小为 $D\times N$ 的矩阵 $\mathbf{X}$ 的运算。$value$,$query$ 和 $key$ 可分别计算如下:
\[\mathbf{V[X]=\beta_v 1^T + \Omega_v X} \\ \mathbf{Q[X]=\beta_q 1^T + \Omega_q X} \\ \mathbf{K[X]=\beta_k 1^T + \Omega_k X}\]这里 $\mathbf{1}$ 是一个 $N\times 1$ 的全1矩阵用来同一维度,相应的,自注意力计算可以表示为:
\[\mathbf{Sa[X]}=\mathbf{ V[X] \cdot Softmax [ K[X]^T Q[X] ] }\]这里 $\mathbf{Softmax[\bullet]}$ 是对所得矩阵的每一列进行作用(如果将 $\mathbf{q_n}$ 对应一个列向量,那么可以将 $\mathbf{K}$ 与其作用的结果也对应为一个列向量)。
位置编码
不难看出我们上述的分析过程并没有考虑不同输入之间的先后次序关系,但是就像我们之前的例子所说的,相同的单词在不同的位置所表达的含义可能是不一样的,这表明一个输入的顺序信息是决定其表达含义的非常重要的因素,因此我们引入位置编码(position encoding)来引入位置信息。
绝对位置编码(absolute position embeddings):矩阵 $\mathbf{\Pi}$ 被添加到输入 $\mathbf{X}$ 之中,对位置信息进行编码,矩阵中的每一列都是唯一的,因此包含了关于输入序列中位置的信息。这个矩阵可以手工选择,也可以学习。可以被添加到网络输入,或者添加到每一层之中。有时,它在对 $query$ 和 $key$ 进行计算的时候被添加到 $\mathbf{X}$ 中,但是在计算 $value$ 的时候并不添加。
相对位置编码(relative position embeddings):有时其输入可以是一个完整的句子或者许多句子,单词的绝对位置远不如两个输入之间的相对位置重要。相对位置编码为两个位置之间学习一个参数 $\pi_{a,b}$,并使用它来修改注意力矩阵(如相加或相乘等方式)。
点积缩放
注意力计算中的点积结果的幅度较大,使得 softmax 之后,原始点积结果的最大值完全占据主导地位,输入的变化对输出几乎没有影响,这使得梯度非常小,模型难以训练。为了防止这种情况,点积按照 $key$ 和 $query$ 的维度的平方根进行缩放:
\[\mathbf{Sa[X] = V \cdot Softmax} [ \frac{\mathbf{K^T Q}}{\sqrt{D_q}} ]\]多头注意力机制
我们常常将多个注意力块并行投入使用,这一机制即多头注意力机制(multi-head self-attention),我们假定需要计算 $H$ 个不同种类的 $value$,$key$ 和 $query$:
\[\mathbf{V_h=\beta_{vh} 1^T + \Omega_{vh} X} \\ \mathbf{Q_h=\beta_{qh} 1^T + \Omega_{qh} X} \\ \mathbf{K_h=\beta_{kh} 1^T + \Omega_{kh} X}\]第 $h$ 个 $head$ 的自注意力过程可以表示为:
\[\mathbf{Sa_h[X] = V_h \cdot Softmax} [ \frac{\mathbf{K^T_h Q_h}}{\sqrt{D_q}} ]\]一般来说,如果输入 $\mathbf{x_m}$ 的维度是 $D$ ,注意力头的个数是 $H$ ,$value$,$key$ 和 $query$ 的大小为 $D/H$,自注意力头的输出矩阵垂直连接起来,再经过一个线性变换 $\mathbf{\Omega_c}$ 得到最终输出:
\[\mathbf{MhSa[X]=\Omega_c \left[ Sa_1[X]^T,Sa_2[X]^T,...,Sa_H[X]^T \right] ^T}\]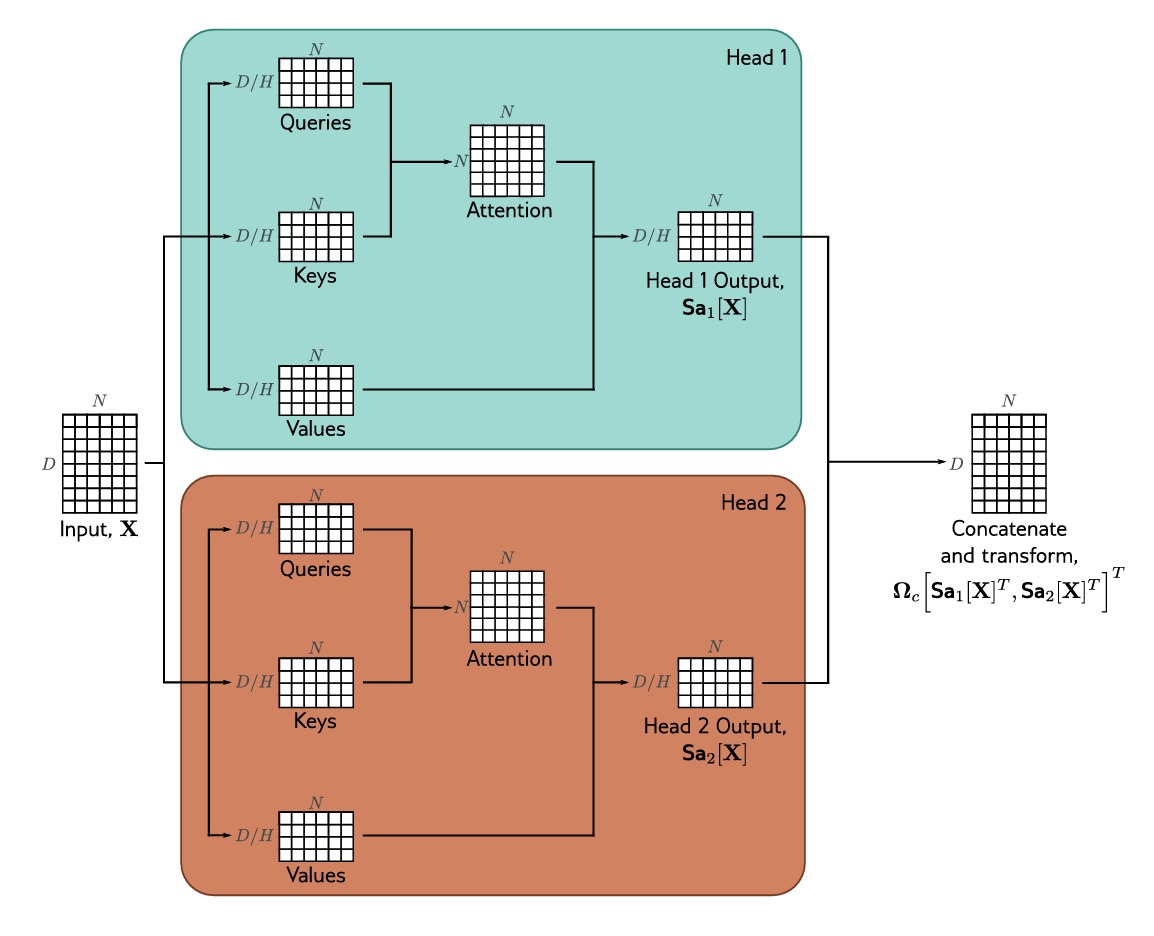
上图揭示了多头注意力机制的运作过程。
整体来看,一个transformer层的组成可以由如下过程构成:
\[\mathbf{X \larr X + MhSa[X]} \\ \mathbf{X \larr LayerNorm[X]} \\ \mathbf{x_n \larr x_n + mlp[x_n]} \\ \mathbf{X \larr LayerNorm[X]}\]输入首先通过一个多头注意力模块,然后是一个全连接网络MLP,这两个部分都是残差网络(即输出被添加回原始输入),此外通常在自注意力模块和MLP之后添加LayerNorm操作。
Encoder示例:BERT
BERT是一个编码器模型,使用了30000个 $token$ 的词汇表,输入标记被转换为1024维的 $embedding$ ,并通过24个 transformer 层,每个层均为有16个头的自注意力机制,每个头的 $value$,$key$ 和 $query$ 均为64维。
预训练
预训练阶段使用自监督进行训练,这允许在不需要手动标签的情况下使用大量数据。对于BERT来说,自监督任务包括预测大型互联网语料库中的缺失单词。
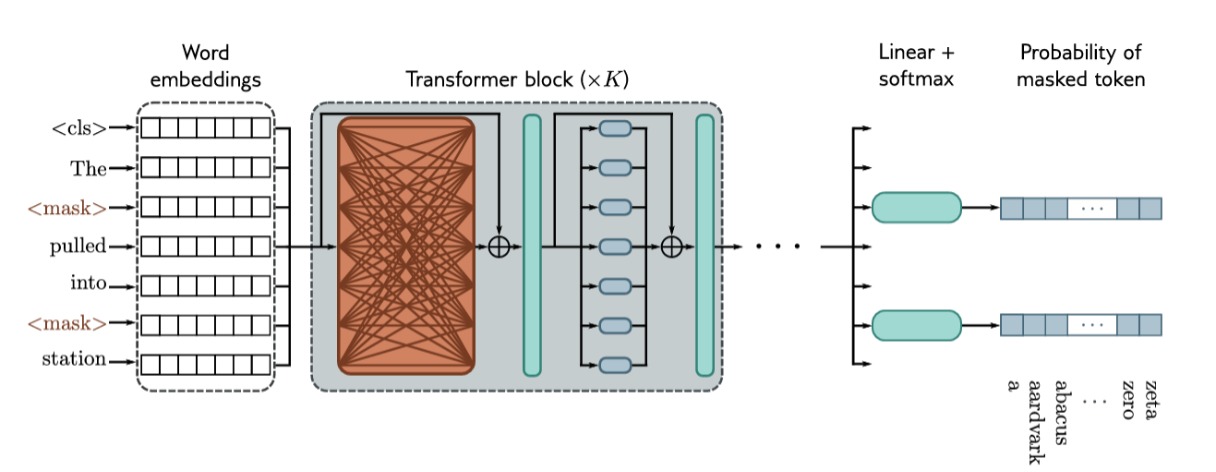
如图所示,输入 $token$ 被转换为 $embedding$ ,之后通过一系列 transformer 层(橙色表示每个 $token$ 都关注其他输入 $token$)来得到输出 $embedding$ 。一小部分输入 $token$ 被随即替换为通用的 $\lt Mask\gt$ 。在预训练中,目标是从相关的输入中预测缺失的单词,因此输出 $embedding$ 通过 $softmax$ 函数,并使用多类分类损失。在图中我们可以看到,网络处理了7个 $token$,并对选择的2个位置进行预测。
Fine-tuning
Fine-tuning 的概念来自于迁移学习,利用神经网络强大的泛化能力进行小数据的训练,可以理解为站在了巨人的肩膀上。在 Fine-tuning 阶段,调整模型参数使得网络专门用于特定任务,并加入额外的层,将输出向量转换为所需要的输出格式。
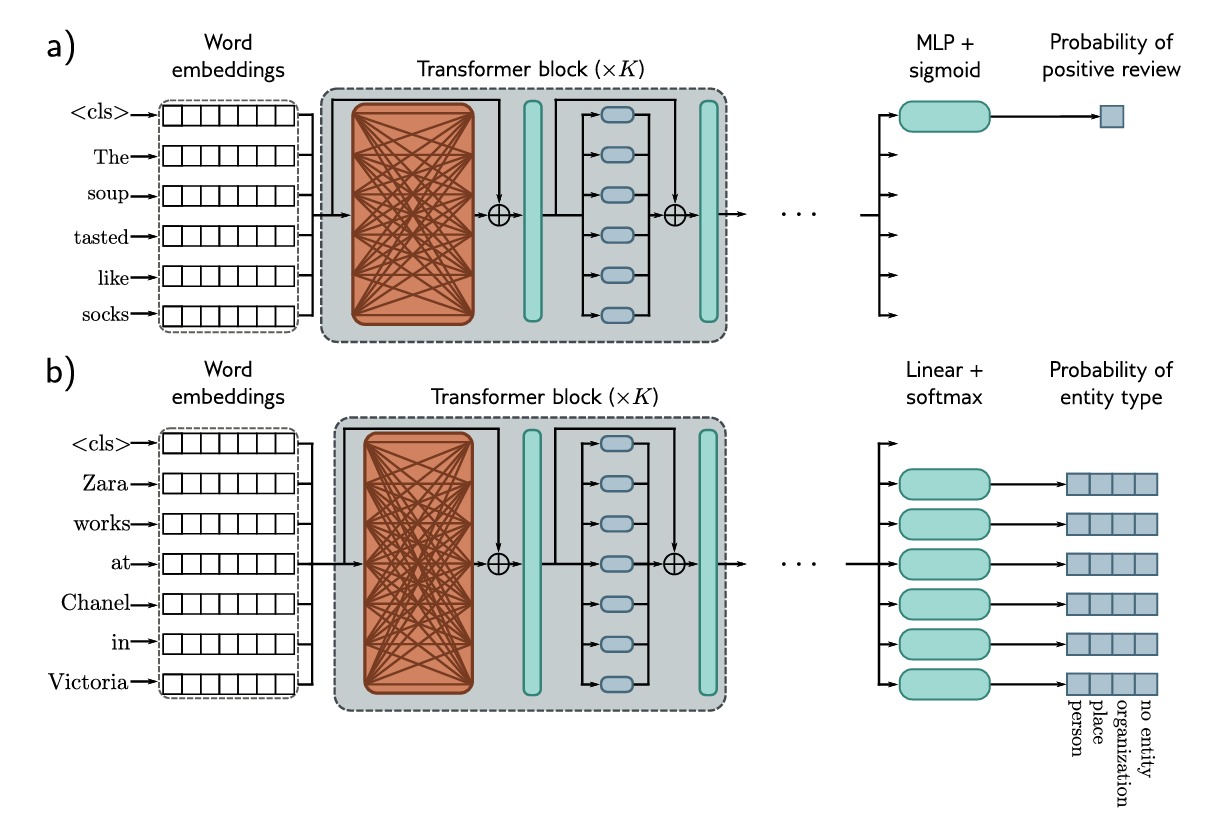
文本分类:如上图a)所示,在预训练期间加入 $\lt cls \gt$ 作为特殊的 $token$ 放置在每个句子的开头。对于一些文本分类任务,如情感分析,与 $\lt cls\gt$ 对应的向量会映射到一个数字上,这用来标识我们分类的结果。
单词分类:如上图b)所示,将每个单词分类为一个实体类型(如个人、地点、组织或无实体)。为此,将每个输入嵌入 $\mathbf{x_n}$ 映射到 $K \times 1$ 向量,其中 $K$ 为不同类别,通过softmax函数得到每个类别的概率。
Decoder示例:GPT3
GPT3是解码器模型的一个示例,其基本架构与编码器模型极其相似,并包括一系列对学习单词 $embedding$ 进行操作的 transformer 层。但是其目标与编码器不同,编码器旨在构建文本的表示,并对其进行微调,而解码器是为了生成序列中的下一个 $token$ ,它通过将扩展序列反馈到模型中来生成连贯的文本段落。
语言模型
GPT3是一个自回归的语言模型,它将N个 $token$ 的联合概率 $Pr(t_1,t_2,…,t_N)$ 转化为自回归序列:
\[Pr(t_1,t_2,...,t_N)=Pr(t_1) \prod_{n=2}^{N} Pr(t_n|t_1,...,t_{n-1})\]也即将一个句子中的若干 $token$ 连续出现的概率,转化为下一个 $token$ 在之前的 $token$ 基础上的条件概率乘积。
掩码自注意力机制
我们可以看到我们将文本的输出作为 $token$ 出现的概率来表征,训练解码器是一个自回归的过程,这个过程以最大化输入文本的概率为目标。理想情况下,我们会输入整个句子,然后同时计算所有的对数概率和梯度。然而这有一个问题,如果我们输入完整的句子,那么系统在预测下一个的时候,不仅会看到这个单词之前的内容,还可以看到这个单词之后的内容,这样我们无法判断它是不是通过这个单词前面的内容来预测的,从而更加说明它在实际预测的过程中真的有效。
我们引入掩码自注意力机制(masked self-attention)来解决这一问题。由于 $token$ 只在自注意力层中进行彼此之间的交互,因此我们可以设置预测的过程中对后续的 $token$ 的注意力为0,要实现这一点,可以在通过 $\mathbf{Softmax[\bullet]}$ 函数之前将注意力计算中的相应点积设置为负无穷大。
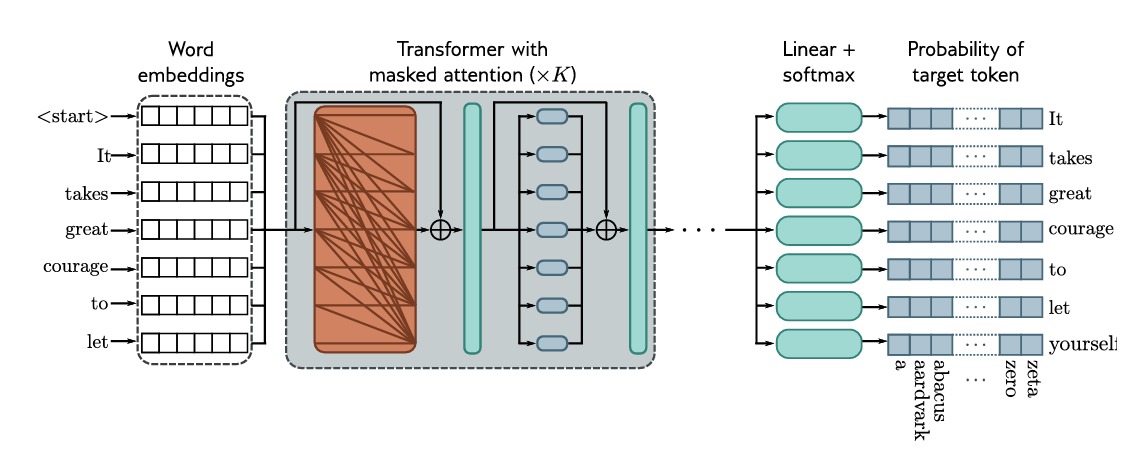
如图所示,整个解码器网络的操作即:输入文本被标记化并被转换为 $embedding$ ,然后被传递到 transformer 网络中。由于现在使用了掩码自注意力机制,因此它们只能关注现在和之前的 $token$。每个输出 $embedding$ 的目标是预测序列中的下一个 $token$,因此在 transformer 层之后,通过一个线性层将输出 $embedding$ 映射到词汇表的大小,并通过 $\mathbf{Softmax[\bullet]}$ 将其转换为一种概率分布。我们的目标就是使用交叉熵损失,在已知前面序列的情况下最大化下一个 $token$ 应当出现的概率。
GPT3
GPT3大规模地应用了上述的思想,序列长度为2048个 $token$,并且由于同时处理2048个 $token$ 的多个跨度,因此总批量大小为320万个 $token$。有96个transformer层,每个层处理大小为12288的单词 $embedding$。每个自注意力层中有96个 $head$,并且 $value$,$key$ 和 $query$ 的维度是128。它使用3000亿个 $token$ 进行训练,包含1750亿个参数。
Encoder-Decoder示例:机器翻译
语言之间的翻译是 $sequence-to-sequence$ 任务的一个例子,这需要一个编码器(计算原始句子的中间表示)和一个解码器(以目标语言生成句子),这个任务即典型的 Encoder-Decoder 模型。
比如一个从英语翻译到法语的模型,Encoder接受一个英语句子作为输入,并为每个 $token$ 生成其对应的 $embedding$。在训练过程中,Decoder接受ground truth法语句子作为输入,将其送入一系列 transformer 层,并使用掩码自注意力机制让其预测下一个单词。然而,Decoder同时也需要关注Encoder的输出,这样最终每一个法语单词才将是同时结合了输入英语信息和此前翻译的法语的单词,这一过程称为交叉注意力机制(cross-attention)。
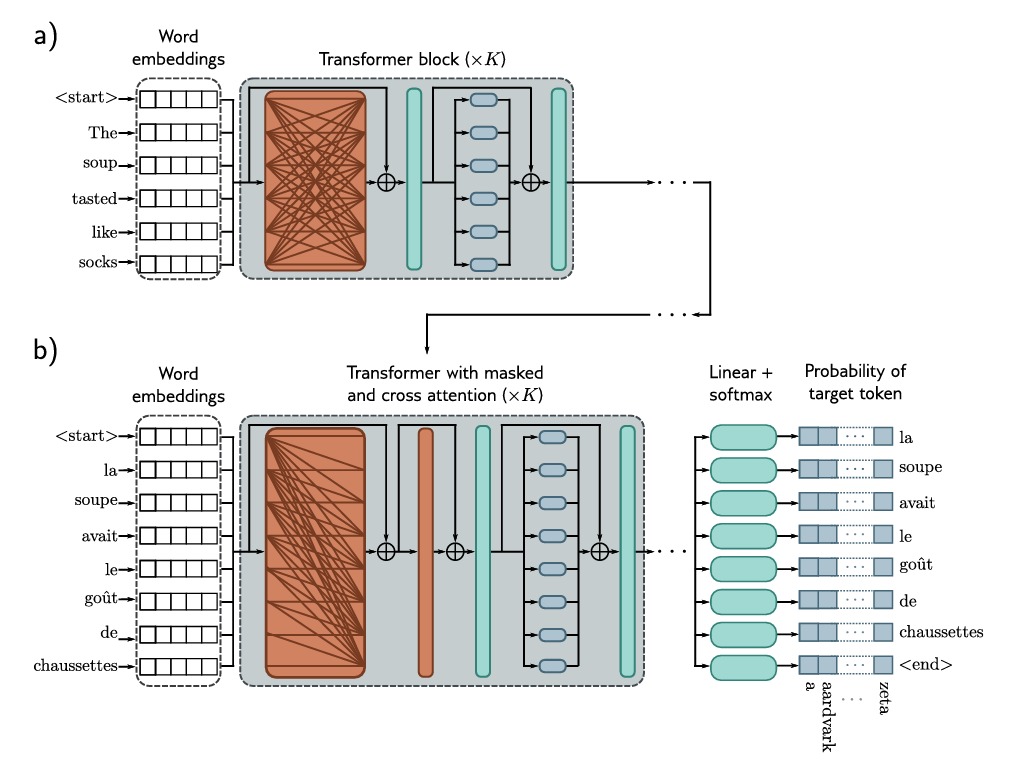
如图所示,两个句子被送入模型中,目的是将第一句翻译成第二句,a)图中,第一句话通过Encoder编码,b)图中,第二句话通过Decoder,它使用掩码自注意力机制,但也使用交叉注意力机制来处理编码器的输出 $embedding$,我们希望通过训练使得Decoder正确输出下一个单词的概率最大化。
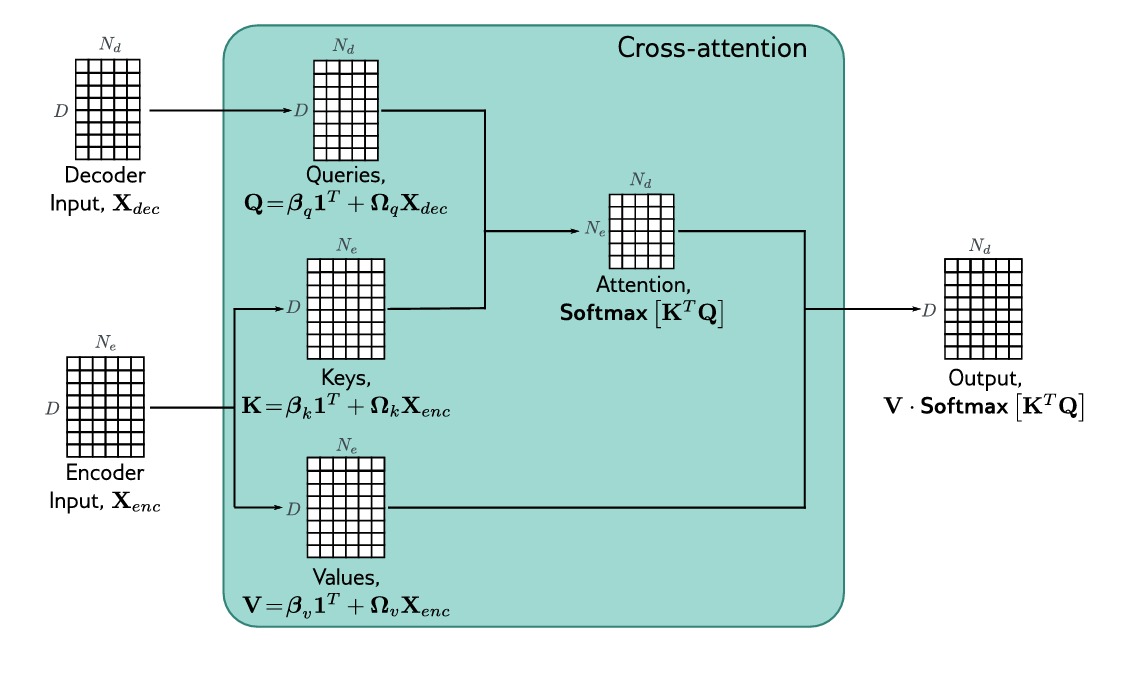
这里再解释一下何为交叉注意力机制,这是通过修改Decoder中的transformer层来实现的。Decoder中的原始transformer层由一个掩码自注意力层组成,然后是单独应用于每个 $embedding$ 的神经网络,在这两个组件之间我们加入一个新的注意力层,这里Decoder的 $embedding$ 关注Encoder的 $embedding$,具体来说,$query$ 是根据Decoder的 $embedding$ 来计算的,而 $value$ 和 $key$ 是通过Encoder的 $embedding$ 来计算的。
参考文献
- 《Understanding Deep Learning》Simon J.D. Prince