本文系MIT深度学习综述手册《Understanding Deep Learning》学习笔记
生成对抗网络(Generative Adversarial Network,GAN)是一个生成模型,它学习所提供的样本,并可以生成不同于训练样本的新结果。其基本思想很简单,由一个判别器和一个生成器组成。主网络通过将随机噪声映射到输出数据空间来生成样本,如果判别器不能区分生成的样本和真实的样本,那么可以说生成的样本是成功的;如果判别器可以判别出差异,那么这就提供了一个可以反馈的训练信号,以提高样本的质量。GAN在图像领域取得了最大的成功,在这里可以生成与真实图片几乎没有区别的样本。
GAN的基本思想
设训练数据为 ${ \mathbf{x_i} } $,我们的目的是生成新的样本 ${ \mathbf{x_i^{\ast}} } $ ,使得新样本和原始数据无法分辨。一个新样本 $\mathbf{x}_{j}^{\ast}$ 的生成过程大致为,首先从简单的基本分布(如标准正态分布)中选择一个隐变量(latent variable)$\mathbf{z}_j$ ,然后放到网络中得到 $\mathbf{x^{\ast}=g[z_j,\theta]}$ ,其中 $\mathbf{\theta}$ 是网络参数。这个网络即生成器(generator),网络学习的目标是找到最好的 $\mathbf{\theta}$ ,使得生成的样本看起来和真实原始数据非常相似。
GAN对相似度的评价方式是,能否将生成的结果和原始真值区分开来。为了这个目的,我们引入第二个网络 $f[\bullet , \phi]$ ,此网络即判别器(discriminator),其中 $\phi$ 为网络参数。这个网络的目标是将输入分类为是一个真实样本还是生成结果。如果我们已经无法区分,那么我们可以说生成的样本是成功的。如果仍然可以区分,那么判别器将会提供一个信号来提高生成效果。
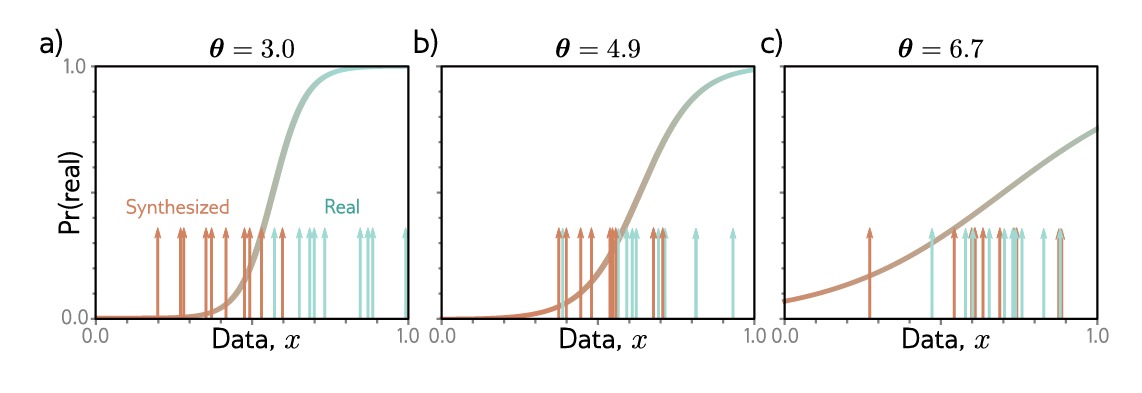
如图所示,我们以一维训练集 ${x_i}$ 开始,一个batch中含有十个样例(图中的蓝色箭头),为了生成一个batch的新样本,我们使用如下的简单生成方式:
\[x_j^*=g[z_j,\theta]=z_j + \theta\]这里隐变量 ${z_j}$ 是从标准正态分布中选取的,参数 $\theta$ 即沿x轴方向进行平移。当初始化$\theta = 3.0$ 时,生成的样本(橙色箭头)位于真实样本的左部,判别器被训练为将生成的样本和真实样本区分开来, 这里的 sigmoid 曲线即表示了这个样本是否为真实样本的概率。在训练过程中,生成器参数 $\theta$ 得到反馈并且自增,以增加样本被分类为真实样本的概率。
我们交替更新判别器和生成器。上图中的b)和c)展示了两个迭代过程。将样本进行区分变得越来越困难,因此使 $\theta$ 增加的动力变得越来越弱(如图 sigmoid 函数变得更加平坦)。在最后,已经无法分辨二者,我们可以丢下判别器,并得到一个可以乱真的生成器。
损失函数
我们现在定义一个损失函数,来更加精确地训练GAN。我们用 $f[\mathbf{x,\phi}]$ 来表示判别器,它以 $\mathbf{x}$ 作为输入,参数为 $\phi$ ,并且返回输入为真的概率。这是一个二元分类任务,我们引入二元交叉熵损失函数:
\[\hat{\phi} = \mathop{\arg\min}_{\phi} \left[ \sum_i -(1-y_i)log\left[ 1- sig[f[\mathbf{x,\phi}]] \right] -y_i log \left[ sig[f[\mathbf{x,\phi}]]\right] \right]\]这里 $y_i \in {0,1 }$ 是判别的结果,$sig[\bullet]$ 是logistic sigmoid函数,如图所示,我们假定真实样本 $\mathbf{x}$ 对应 $y=1$,生成样本 $\mathbf{x}^*$ 对应 $y=0$,因此有:
\[\hat{\phi} = \mathop{\arg \min}_{\phi} \left[ \sum_j -log\left[ 1-sig[f[\mathbf{x_j^*,\phi}]]\right] - \sum_i log\left[ sig[f[\mathbf{x_i,\phi}]]\right] \right]\]其中 $i$ 和 $j$ 对应真实样本和生成样本的索引。
现在我们将生成器的定义替换为 $\mathbf{x_j^*=g[z_j,\theta]}$ 并且我们希望找到 $\mathbf{\theta}$ 使得损失结果更大(因为我们希望生成的样本被错误分类):
\[\hat{\phi},\hat{\theta} = \mathop{\arg \max}_{\theta} \left[ \mathop{\min}_{\phi} \left[ \sum_j - log\left[1-sig[f[\mathbf{g[z_j,\theta],\phi}]] \right] -\sum_i log\left[ sig[f[\mathbf{x_i,\phi}]] \right] \right] \right]\]训练GAN
GAN训练被描述为 $minimax\ \ game$,生成器试图找到欺骗判别器的新方法,判别器反过来寻找新方法来区分生成的样本和真实示例。理论上来说,解决方案是一个是一个纳什均衡——优化算法搜索一个位置,该位置同时是一个函数的最小值和另一个函数的最大值。如果训练如期进行,那么收敛后 $\mathbf{g[z,\theta]}$ 将从与训练数据相同的分布中提取,然后 $sig[f[\mathbf {\bullet,\phi}]]$ 将会接近随机(即概率0.5)。
为了训练GAN,我们可以将前式分解为两个损失函数:
\[\begin{array}{l} L[\phi] = \sum\limits_{j} -log\left[1-sig[f[\mathbf{g[z_j,\theta],\phi}]] \right] - \sum\limits_i log\left[ sig[f[\mathbf{x_i,\phi}]]\right] \\ L[\theta] = \sum\limits_j log\left[ 1-sig[f[\mathbf{g[z_j,\theta],\phi}]]\right] \end{array}\]在第二个函数中,我们取负并且舍弃无关项,使得我们的损失函数目标都是最小化。最小化第一个函数来训练判别器,最小化第二个函数来训练生成器。
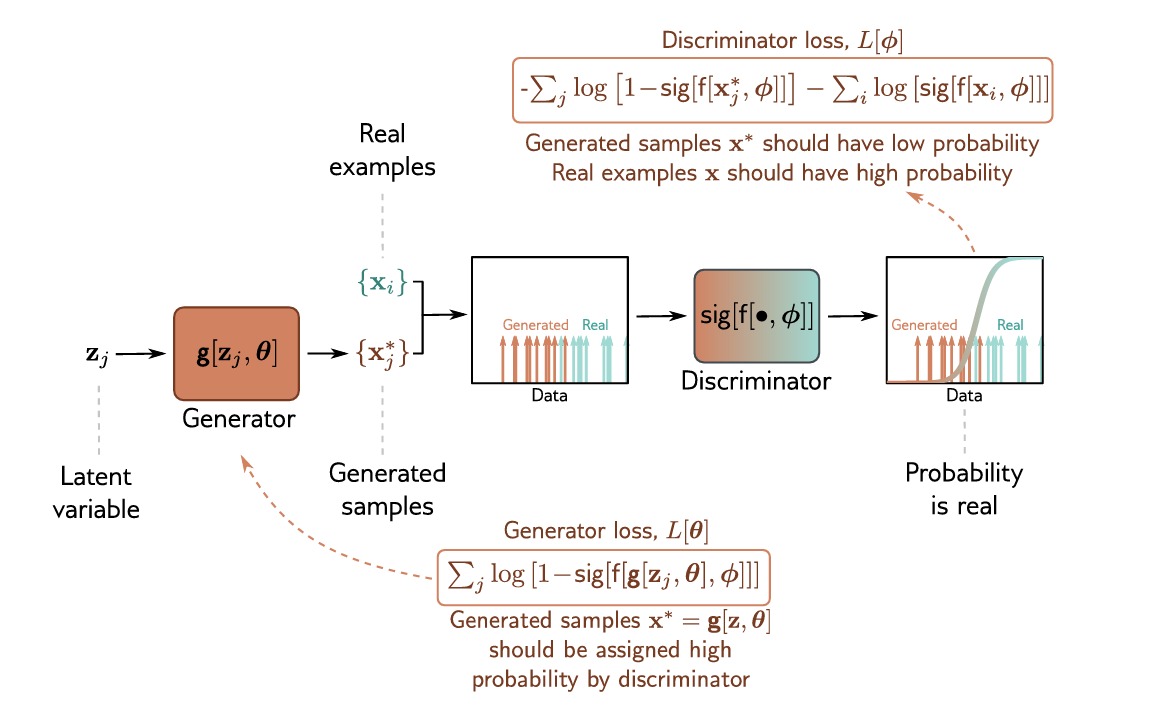
如上图,在每一步,我们都从基本分布中选择一个bacth的隐变量 $\mathbf{z}_j$ 并将其送入生成器,得到生成样本 $\mathbf{x_j^*=g[z_j,\theta]}$ 。然后我们选择一个batch的真实样本 $\mathbf{x}_i$ ,得到这两个batch,我们可以对每个损失函数执行一个或者多个梯度下降步骤。
深度卷积GAN
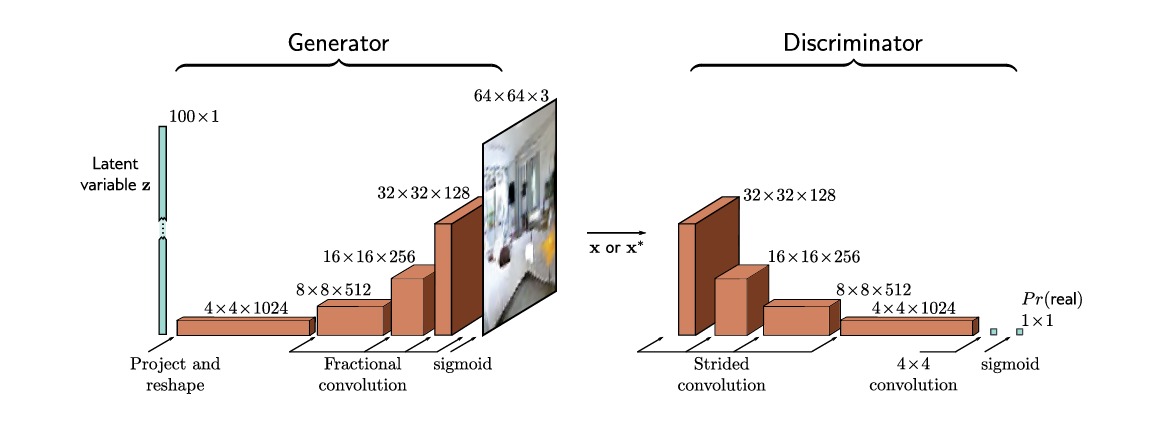
深度卷积对抗神经网络(deep convolutional GAN,DCGAN),是一个用于生成图片的较早的GAN结构。生成器的输入是一个从标准分布中选取的100维的隐变量 $\mathbf{z}$ ,之后使用线性映射将其映射到一个具有1024个通道的 $4\times4$ 的空间表示。后面是4个卷积层,每个卷积层都使用分数步长,使得分辨率翻倍(即步长为0.5的卷积)。在最后一层中,这个 $64\times 64\times 3$ 的信号通过一个 arctan 函数来生成一个分布在 $[-1,1]$ 的图片 $\mathbf{x}^*$ 。
判别器是一个标准卷积神经网络,其最后一个卷积层将大小降低到单通道的 $1\times 1$ 大小。这个数字后面通过一个 sigmoid 函数来得到输出的概率。在训练之后,判别器就被丢弃,我们只需要从基本分布中选择隐变量通过生成器生成结果。
训练GAN的困难
GAN很难训练,为了让DCGAN可靠地训练,一般的措施如下:
- 使用跨步卷积进行上采样和下采样;
- 在生成器和判别器中,除了最后一层和第一层,都分别使用 BatchNorm;
- 在判别器中使用Leaky ReLU激活函数;
- 使用Adam优化器,但动量系数比平时低;
一个常见的失败模式是生成器会生成似是而非的样本,但是仅限于训练数据的子集(例如对于人脸,它可能永远不会生成有胡须的人脸),这称为模式丢弃(mode dropping)。这种现象的一个极端版本是生成器完全忽略输入变量 $\mathbf{z}$ 并将所有样本折叠到一个或几个点,这被称为模式崩溃(mode collapse)。
提高稳定性
要理解为什么GAN难以训练,有必要准确理解损失函数的含义。
损失函数分析
我们先来介绍KL散度(Kullback-Leibler divergence),它常常用来衡量两个概率分布之间的距离,其定义如下所示:
\[D_{KL} \left[ p(x)||q(x)\right] = \int p(x) \log \left[ \frac{p(x)}{q(x)} \right]dx\]这个距离总是大于等于零,我们可以利用 $-\log \left[ y \right] \ge 1-y$ 来证明如下:
\[\begin{array}{l} D_{KL} \left[ p(x)||q(x) \right] & = & \int p(x) \log \left[ \frac{p(x)}{q(x)} \right]dx \\ & = & -\int p(x) \log\left[ \frac{q(x)}{p(x)} \right] dx \\ & \ge & \int p(x) \left( 1- \frac{q(x)}{p(x)} \right)dx \\ & = & \int p(x)-q(x) dx \\ & = & 1-1=0 \end{array}\]当 $q(x)$ 为 0 而 $p(x)$ 不为 0 的时候,KL散度将为无穷,这将使得它作为一个距离度量相当不稳定。而且KL散度还有一个缺点是它并不是对称的,为此我们引入JS散度(Jensen-Shannon divergence),它是KL散度两个方向的平均:
\[D_{JS} \left[ p(x)||q(x) \right] = \frac{1}{2} D_{KL} \left[p(x)||\frac{p(x)+q(x)}{2} \right] + \frac{1}{2} D_{KL} \left[q(x)||\frac{p(x)+q(x)}{2} \right]\]我们现在回顾损失函数 $L[\phi]$ ,并分别对 $i,j$ 的损失取平均,我们可以得到损失函数的期望形式:
\[\begin{array}{l} L[ \phi] & = & \frac{1}{J} \sum\limits_{j=1}^{J} \left( \log\left[1-sig[f[\mathbf{x_j^*,\phi}]]\right] \right) + \frac{1}{I} \sum\limits_{i=1}^I \left(\log\left[ sig[f[\mathbf{x_i,\phi}]]\right] \right) \\ & \approx & \mathbb{E}_{\mathbf{x}^*} \left[\log\left[1-sig[f[\mathbf{x^*,\phi}]]\right]\right] + \mathbb{E}_{\mathbf{x}^*} \left[\log\left[sig[f[\mathbf{x^*,\phi}]]\right]\right] \\ & = & \int Pr(\mathbf{x}^*) \log \left[1-sig[f[\mathbf{x^*,\phi}]]\right]d\mathbf{x}^* + \int Pr(\mathbf{x}) \log \left[sig[f[\mathbf{x,\phi}]]\right]d\mathbf{x} \end{array}\]其中 $Pr(\mathbf{x^*})$ 是生成样本的概率分布,而 $Pr(\mathbf{x})$ 是真实样本的概率分布。最佳的判别器应当取值如下:
\[Pr(\mathbf{x}\ \ is \ \ real)=sig[f[\mathbf{x,\phi}]] = \frac{Pr(\mathbf{x})}{Pr(\mathbf{x}^*) + Pr(\mathbf{x})}\]即此处样本为真实样本的概率,等价于此处样本为真的分布占总分布的比例。将其带入前面的推导,可以得到:
\[\begin{array}{l} L[\phi] &=& \int Pr(\mathbf{x}^*)\log \left[1-sig[f[\mathbf{x^*,\phi}]]\right]d\mathbf{x}^* + \int Pr(\mathbf{x})\log \left[sig[f[\mathbf{x,\phi}]]\right]d\mathbf{x} \\ &=& \int Pr(\mathbf{x}^*) \log\left[1-\frac{Pr(\mathbf{x})}{Pr(\mathbf{x}^*)+Pr(\mathbf{x})} \right]d\mathbf{x}^* + \int Pr(\mathbf{x}) \log\left[\frac{Pr(\mathbf{x})}{Pr(\mathbf{x}^*)+Pr(\mathbf{x})} \right]d\mathbf{x} \\ &=& \int Pr(\mathbf{x}^*) \log\left[\frac{Pr(\mathbf{x}^*)}{Pr(\mathbf{x}^*)+Pr(\mathbf{x})} \right]d\mathbf{x}^* + \int Pr(\mathbf{x}) \log\left[\frac{Pr(\mathbf{x})}{Pr(\mathbf{x}^*)+Pr(\mathbf{x})} \right]d\mathbf{x} \end{array}\]忽略乘法和加法常数,上式等价于 $Pr(\mathbf{x}^*)$ 和 $Pr(\mathbf{x})$ 之间的JS散度:
\[\begin{array}{l} D_{JS}\left[Pr(\mathbf{x}^*)||Pr(\mathbf{x}) \right] \\ = \frac{1}{2}D_{KL} \left[Pr(\mathbf{x}^*)||\frac{Pr(\mathbf{x}^*)+Pr(\mathbf{x})}{2} \right] + \frac{1}{2}D_{KL} \left[Pr(\mathbf{x})||\frac{Pr(\mathbf{x}^*)+Pr(\mathbf{x})}{2} \right] \\ = \frac{1}{2} \int \underbrace{Pr(\mathbf{x}^*)\log \left[\frac{2Pr(\mathbf{x}^*)}{Pr(\mathbf{x}^*) + Pr(\mathbf{x})} \right]}_{quality} + \underbrace{Pr(\mathbf{x})\log \left[\frac{2Pr(\mathbf{x})}{Pr(\mathbf{x}^*) + Pr(\mathbf{x})} \right]}_{coverage} d\mathbf{x} \end{array}\]这里面的第一项表明,如果希望距离变小,在生成样本密度较大的区域(即 $ Pr( \mathbf{x^{\ast}} )$ 较高),需要让均值 $(Pr(\mathbf{x^{\ast}}) + Pr(\mathbf{x}))/2$ 更高,即它惩罚那些有生成样本却没有真实样本的区域,即提高生成样本的质量(quality)。这里面的第二项表明,如果希望距离变小,在真实样本密度较大的区域(即 $Pr(\mathbf{x})$ 较高),需要让均值 $(Pr(\mathbf{x^{\ast}}) + Pr(\mathbf{x}))/2$ 更高,即它惩罚那些有真实样本却没有生成样本的区域,即提高生成样本的覆盖范围(coverage)。
但是我们发现,负责coverage的项,对应 $L[\phi]$ 的第二项,其中并没有生成样本参与,因此它不依赖于生成器。故而生成器并不关心覆盖范围,从而倾向于生成可能示例的子集。
我们可以看到,理想状况下判别器的损失函数试图最小化生成样本和真实样本之间的距离。然而,使用概率分布之间的这种距离存在一个潜在的问题:如果概率分布完全不相交,那么这个距离是无限的,对生成器的任何小的改变都不会减少损失。这一点也可以直观地理解,如果生成的样本很容易与真实样本区分开来,那么,二者的分布可能相当明显,判别器在生成样本的位置的斜率会很小,更新生成器参数的梯度也就会非常小。
不幸的是,生成的样本和真实样本的分布可能真的是不相交的; 在训练期间,生成样本都位于一个大小为噪声向量 $\mathbf{z}$ 大小的子空间中,并且从影响数据的真实的物理因素而言,真实样本也位于低维子空间中。 这些子空间之间可能很少或没有重叠,结果就会导致非常小或没有梯度。
最优传输距离
前面的部分表明,GAN的损失可以用概率分布之间的距离来解释,并且当生成的样本过于容易与真实样本区分开时,该距离的梯度变为零。因此我们需要选择具有更好属性的距离度量。
我们引入最优传输距离(Wasserstein distance),又称推土机距离,它是将概率质量从一个分布传输到另一个分布所需的工作量。这里的工作量可以类比物理学做功的概念,即质量乘以移动的距离。Wasserstein 距离是明确定义的,即使二者的分布并不相交,仍然可以随着彼此靠近而减小。
对于离散概率分布,Wasserstein 距离最容易理解。考虑在K个盒子上定义的分布 $Pr(x=i)$ 和 $q(x=j)$ ,假设 $ P_{ij} $ 为从第一个分布中的盒 $i$ 移动到第二个分布中的盒 $j$ 的单位质量数,一个单位质量的移动花费可以表示为 $i$ 和 $j$ 距离的绝对值 $|i-j|$。质量移动的方案即被存在矩阵 $\mathbf{P}$ 中。
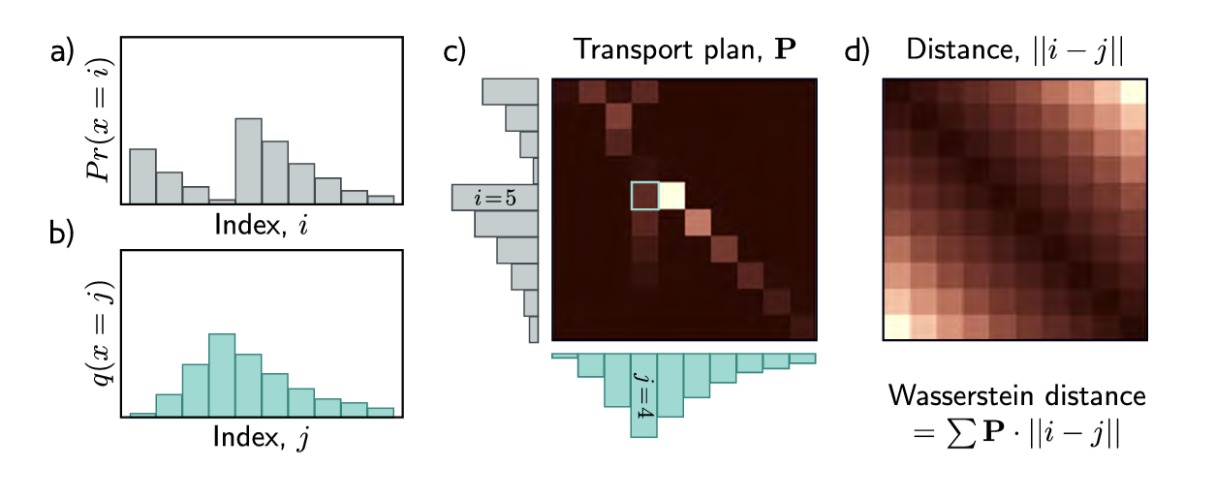
Wasserstein 距离可以表示为:
\[D_{w} \left[Pr(x)||q(x)\right] = \mathop{\min}_{\mathbf{P}} \left[\sum_{i,j} P_{ij}||i-j|| \right]\]且满足如下约束:
\[\begin{array}{c} \sum_j P_{ij} = Pr(x=i) & (initial\ \ distribution \ \ of \ \ Pr(x)) \\ \sum_i P_{ij} = q(x=j) & (initial\ \ distribution \ \ of \ \ q(x)) \\ P_{ij} \ge 0 & (non-negative\ \ masses) \end{array}\]换句话说,Wasserstein距离是将一种分布的质量映射到另一种分布的约束最小化问题的解。这很不方便,因为我们每次想要计算距离时,我们都必须解决元素 $P_{ij}$ 的最小化问题。幸运的是,这是一个标准问题,对于小型方程组很容易解决:这是一个原始形式的线性规划问题(线性规划分为原始形式和对偶形式,如下表)。
| 原始形式 | 对偶形式 |
|---|---|
| $minimize \ \ \mathbf{c^T p},$ | $maximize \ \ \mathbf{b^T q},$ |
| $such\ \ that \ \ \mathbf{Ap=b}$ | $such\ \ that \ \ \mathbf{A^T q\le c}$ |
| $and\ \ \mathbf{p \ge 0}$ |
在这一问题中,$\mathbf{p}$ 的元素即向量化的 $P_{ij}$ ,$\mathbf{c}$ 的元素即距离。$\mathbf{Ap=b}$ 表达了质量分布约束,可以理解为对 $\mathbf{p}$ 中对 $i$ 求和得到的分布应当为初始的质量分布,对 $j$ 求和应当为转化的质量分布,$\mathbf{p\ge 0}$ 保证质量移动非负。
对于所有线性规划问题,存在具有相同解决方案的等效对偶问题,在这里,我们也对上述问题进行转化,从而得到对偶形式如下:我们最大化 $\mathbf{b^T q}$ ,且 $\mathbf{q}$ 受制于距离 $\mathbf{c}$ 的约束。因此这一问题的解可以改写成:
\[D_w \left[Pr(x)||q(x) \right] = \mathop{\max}_{f\bull} \left[\sum_i Pr(x=i)f_i - \sum_j q(x=j)f_j \right]\]并满足约束:
\[|f_{i+1}-f_i| \lt 1\]换句话说,我们优化了一组新的变量 $f_1,…,f_I$,其中相邻值的变化不能超过1。
将这一问题推广到连续问题上,我们可以得到该距离的连续形式:
\[D_w \left[Pr(\mathbf{x},q(\mathbf{x^{\ast}})) \right] = \mathop{\min}_{\pi[\bull,\bull]} \int \int \pi(\mathbf{x_1,x_2}) ||\mathbf{x_1-x_2} || d\mathbf{x_1}d\mathbf{x_2}\]这里的 $\pi [\bull,\bull]$ 代表一种联合分布,和离散情况下的 $\mathbf{P}$ 类似。其对偶形式为:
\[D_w \left[Pr(\mathbf{x},q(\mathbf{x^{\ast}})) \right] = \mathop{\max}_{f[\mathbf{x}]} \left[ \int Pr(\mathbf{x})f(\mathbf{x})d\mathbf{x} -\int Pr(\mathbf{x^{\ast}})f(\mathbf{x})d\mathbf{x} \right]\]受函数 $f[\mathbf{x}]$ 的 Lipschitz 常数小于 1 的约束(即函数的绝对梯度永远不会超过 1)。
我们把Wasserstein 距离应用到GAN上,其生成器的损失函数如下:
\[\begin{array}{l} L[\phi] & = & \sum\limits_j f[\mathbf{x_j^{\ast},\phi}] - \sum\limits_i f[\mathbf{x_i,\phi}] \\ & = & \sum\limits_j f[\mathbf{g[z_j,\theta],\phi}] - \sum\limits_i f[\mathbf{x_i,\phi}] \end{array}\]其中我们必须约束神经网络判别器 $f[\mathbf{x_i},\phi]$ 在每个位置 $\mathbf{x}$ 处具有小于 1 的绝对梯度范数。实现这一点的一种方法是将鉴别器权重限制在一个小范围内(例如,[−0.01,0.01])。 另一种方法是梯度惩罚 Wasserstein GAN 或 WGAN-GP,它添加了一个正则化项,随着梯度范数偏离统一性而增加。
条件生成
GAN 生成逼真的图像但不指定它们的属性:如果不为每种特征组合训练单独的 GAN,我们就无法选择头发颜色、种族或面部年龄。 条件生成模型为我们提供了这种控制。
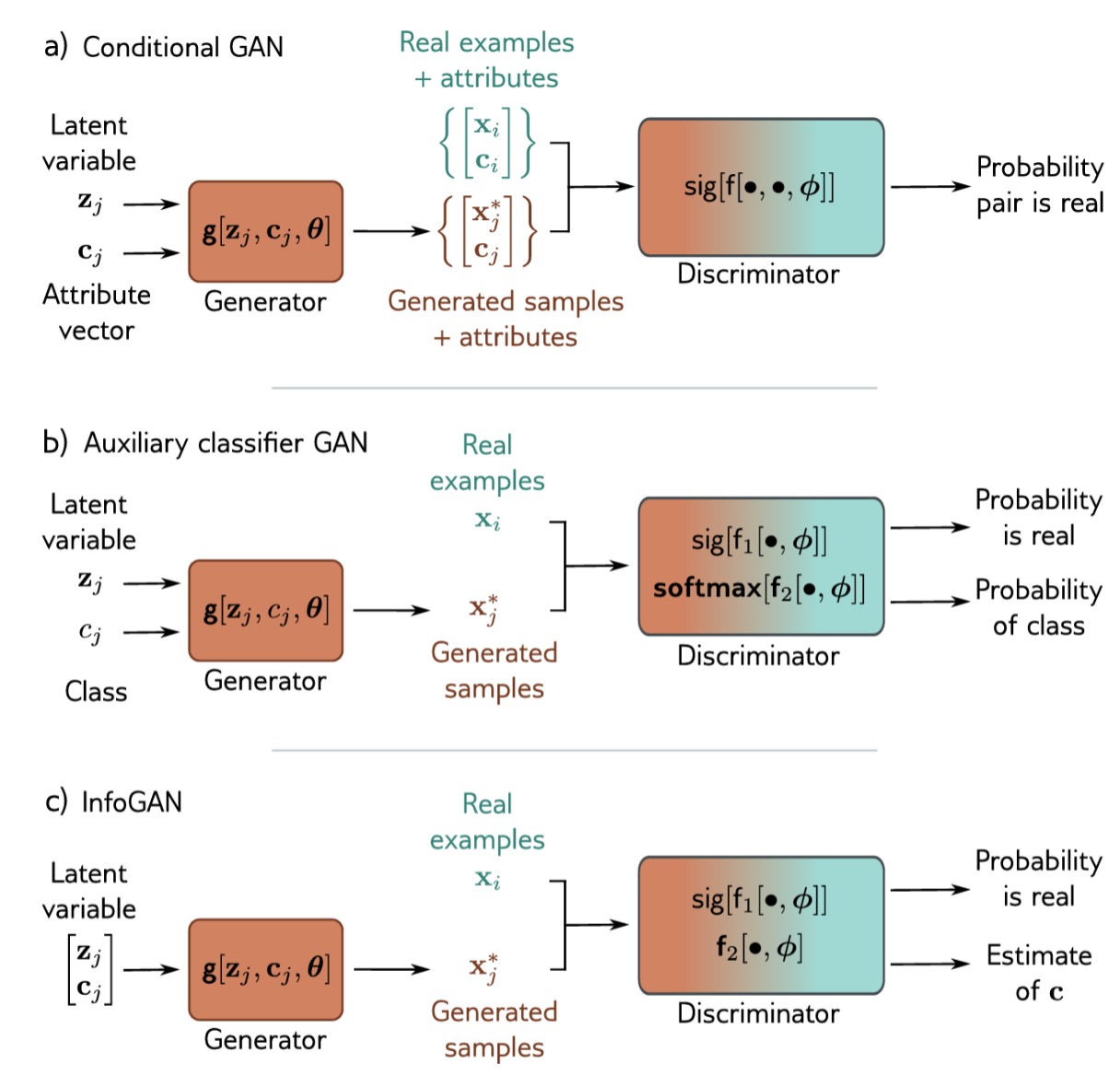
Conditional GAN
如上图a)所示,Conditional GAN 将属性向量 $\mathbf{c}$ 传递给生成器和判别器,现在二者分别写作 $\mathbf{g[z,c,\theta]}$ 和 $\mathbf{f[x,c,\phi]}$ 。生成器旨在将隐变量 $\mathbf{z}$ 转换为具有正确属性 $\mathbf{c}$ 的数据样本 $\mathbf{x}$ 。判别器的目标是区分具有目标属性的生成样本和具有真实属性的真实样本。
对于生成器,属性 $\mathbf{c}$ 可以附加到潜在向量 $\mathbf{z}$。 对于判别器,如果数据是一维的,它可以附加到输入。 如果数据是图像,则可以将属性线性转换为 2D 表示,并作为额外通道附加到鉴别器输入或其中间隐藏层之一。
Auxiliary classifier GAN
如图b)所示,辅助分类器 GAN(Auxiliary classifier GAN,ACGAN),通过要求分类器正确预测属性来简化条件生成。对于离散的有 $C$ 个类别的任务,判别器将真实/生成图像作为输入,并有 $C+1$ 个输出。第一个通过 sigmoid 函数传递并预测样本是生成的还是真实的,其余输出通过 softmax 函数传递,以预测数据属于 $C$ 个类别中每个类的概率。用这种方法训练的网络可以从 ImageNet 中合成多个类。
InfoGAN
Conditional GAN 和 ACGAN 都生成具有预定属性的样本,相比之下,InfoGAN则试图自动识别重要属性。如图c)所示,生成器采用由随机噪声变量 $\mathbf{z}$ 和随机属性变量 $\mathbf{c}$ 组成的向量。判别器预测图像是真实的还是生成的,也估计属性变量。
为什么InfoGAN是有效的,直观的理解就是,如果 $\mathbf{c}$ 的每一个维度对输出都有明确的影响,那么就可以根据输入返回原来的 $\mathbf{c}$。如果没有明显的影响,那么也没法返回。即增加了一个约束,对系统的动力学行为进行了约束,减小了解空间。 $\mathbf{c}$ 中的属性可以是离散的(将使用二元或多类交叉熵损失)或连续的(将使用最小二乘损失)。 离散变量识别数据中的类别,连续变量识别渐进的变化模式。
参考文献
- 《Understanding Deep Learning》Simon J.D. Prince